则有
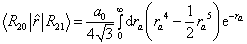（8.3.14）
利用定积分公式
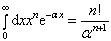（8.3.15）
得到
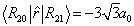（8.3.16）
将径向部分和角度部分的积分值代回矩阵元的表达式，得到
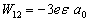（8.3.17）
由微扰算符的厄米性质可知
（8.3.18）
由于
本征函数的正交性可知，量子数 
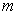不同的态之间的10个矩阵元显然都为零。于是，能量一级修正满足的久期方程为
（8.3.19）
由于，此行列式是准对角的，展开后容易得到
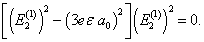（8.3.20）
解上式得到四个解，它们分别为
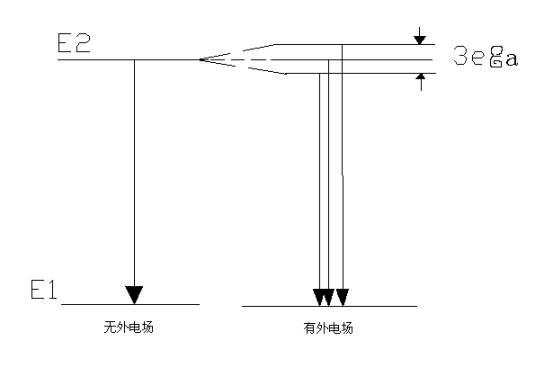
可见，在外电场中，氢原子的第一激发态的能级劈裂成三条，此即氢原子的一级斯塔克效应。如图8.1所示。
|
|
图8.1
一级斯塔克效应
将四个能量的一级修正分别代回本征方程，利用波函数的归一化条件，可以得到零级波函数，这里直接给出结果如下：
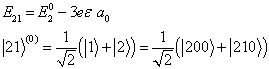（8.3.22）
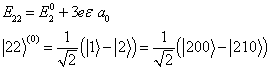（8.3.23）
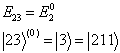（8.3.24）
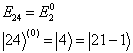（8.3.25）
显然，加上微扰之后，能级仍然存在二度简并。原因很简单，因为微扰算符只含有与
角度相关的项，所以，只能破坏关于
角度的对称性，关于
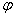角度的对称性仍然存在，故简并不能完全消除。
应该特别说明的是：在应用微扰论处理问题时，通常选用无微扰哈密顿算符的本征矢作为基底，基底的排列顺序（俗称编号）并不影响最后的结果，因此，原则上基底的编号是可以任意选取的。但是，如果排列得当，可能使行列式成为准对角形式的，计算会变得简单。