§8.4 变分法
§8.4.1 变分法
除了微扰论之外，变分法是又一个具有实用价值的近似方法。它的优点在于，不要求算符
的作用远小于算符
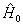，对基态的计算比较精确。在原子与分子物理学中，变分法占有相当重要的地位。
1.
薛定锷方程的变分原理
一个物理体系（无论经典还是量子体系）的动力学方程总可以通过给定体系的拉格朗日量或哈密顿量，用最小作用量原理通过对相应的变量变分后取极小值得出。在经典力学中，这些变量是广义坐标和广义动量。在量子力学中，这些变量是波函数。由此量子力学中定态薛定锷方程可在归一条件下由哈密顿量的平均值对波函数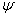 
的极值条件得出。
由
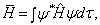（8.4.1）
及归一条件
.
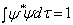（8.4.2）
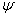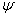再注意到 是复数， 与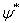 
可视为独立变量，由 
在约束条件（8.4.2）式下的极值条件得
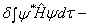
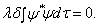（8.4.3）
其中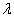 
是约束条件（8.4.2）式的拉格朗日不定乘子。由（8.4.3）及
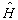的厄米性，得
（8.4.4）
由于
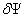和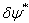 
是任意的变分函数，于是得
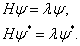（8.4.5）
将拉格朗日不定乘子 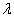看作是体系的能量本征值,则我们就由变分原理导出了定态薛定锷方程。
同样也可以证明，满足薛定锷方程的归一化本征函数，必然使体系平均能量，即相应于本征态的本征能量取极小值。薛定锷方程
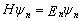（8.4.6）
在归一条件
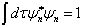（8.4.7）
下，对波函数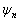 
及 
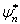作变分，
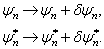（8.4.8）
由
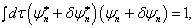（8.4.9）
得
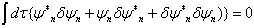
或
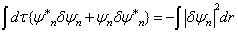（8.4.10）