由此， 
态平均能量或能量本征值 
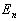的变化是
（8.4.11）
可见
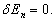（8.4.12）
从而证实，满足薛定锷方程的本征函数，使本征能量 
取极小值。可见，薛定锷方程与量子力学的变分原理等价。
1、有关变分的三个定理
设定态薛定谔方程
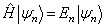
的解为分立谱，
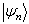是正交归一完备本征矢，将能量本征值按从小到大的顺序排列，即
则哈密顿算符
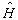的平均值满足如下三个定理(井孝功,
量子力学,
第九章)：
定理1
在任意的归一化的状态 
之下，总有
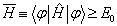（8.4.13）
当
时，
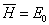，其中，
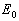为准确的基态能量。
证明：
利用
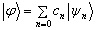（8.4.14）
得到
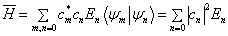（8.4.15）
由于， 
已经归一化，所以，有
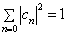（8.4.16）
于是，（8.4.15）可以写为
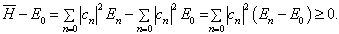(8.4.17)
（8.4.13)成立.
若体系的基态
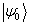已知，则可以利用下面给出的定理2求出第一激发态能量和相应的波函数。
定理2
在任意的归一化的且与
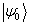正交的状态 之下，总有
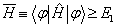（8.4.18）
当 
时，
，其中，
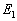为准确的第一激发态能量。