例题8.2
两个自旋为 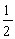 、固有磁矩分别为
、固有磁矩分别为 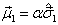 和
和 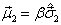 的粒子,处于均匀磁场
的粒子,处于均匀磁场 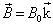 中,若粒子之间的相互作用
中,若粒子之间的相互作用  可视为微扰,求体系能量的二级近似。其中,
可视为微扰,求体系能量的二级近似。其中, 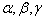 为实常数。
为实常数。
解:体系的哈密顿算符为
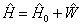 (1)
(1)
其中,
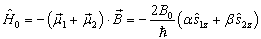 (2)
(2)
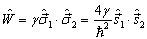 (3)
(3)
在非耦合表象中,基底编号选为
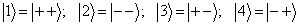 (4)
(4)
这时,算符 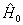 是对角矩阵,其本征值就是对角元,即
是对角矩阵,其本征值就是对角元,即
 (5)
(5)
显然,
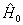 的的解是无简并的,故可以直接利用无简并微扰论公式进行计算。
的的解是无简并的,故可以直接利用无简并微扰论公式进行计算。
在
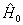 表象中,不为零的微扰算符矩阵元为
表象中,不为零的微扰算符矩阵元为
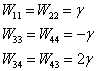 (6)
(6)
利用无简并微扰论公式,
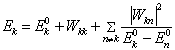 (7)
(7)
得到近似到二级的能量本征值为
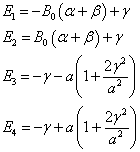 (8)
(8)
此问题的精确解可由下面行列式得到
 (9)
(9)
考虑到(5),解(9)得
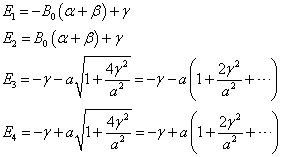 (10)
(10)
其二级近似与(8)式完全一致。