例题8.3
耦合谐振子的哈密顿算符为
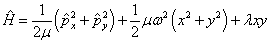
若
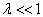 ,试用微扰论求其第一低激发态的能级与本征函数。
,试用微扰论求其第一低激发态的能级与本征函数。
解:若选
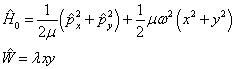 (1)
(1)
则
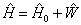 (2)
(2)
已知 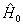 的本征解为
的本征解为
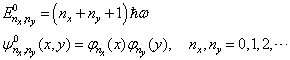 (3)
(3)
令
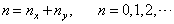 (4)
(4)
则零级近似能量本征值可写成
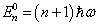 (5)
(5)
为了看清能级的简并情况,将 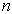 与
与 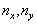 的关系列在下面:
的关系列在下面:
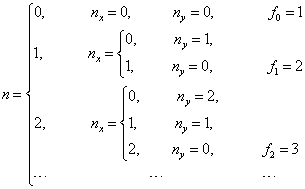 (6)
(6)
显然,第
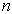 能级的简并度
能级的简并度
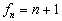 (7)
(7)
第一激发态是 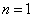 ,简并度为
,简并度为 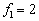 。在简并子空间中,相应的零级近似解为
。在简并子空间中,相应的零级近似解为
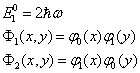 (8)
(8)
能量一级修正满足的本征方程为
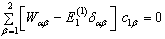 (9)
(9)
相应的久期方程为
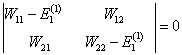 (10)
(10)
利用公式
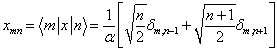 (11)
(11)
式中,
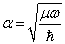 (12)
(12)
可以求出微扰矩阵元
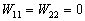 (13)
(13)
而
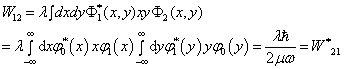 (14)
(14)
将(13)和(14)的矩阵元代入久期方程(10),得到
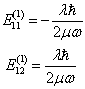 (15)
(15)
显然,能量一级修正已使第一激发态的能级劈裂成两条能级,即将二度简并完全消除。
为了求出近似本征矢,将 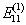 代回本征方程
代回本征方程
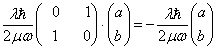 (16)
(16)
得到
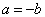 (17)
(17)
由归一化条件可知
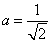 (18)
(18)
于是,得到相应的零级本征矢为
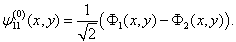 (19)
(19)
同理可得, 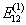 相应的零级本征矢为
相应的零级本征矢为
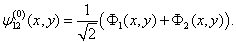 (20)
(20)