例题8.4
一个转动惯量为
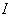 ,电偶极矩为
,电偶极矩为  的平面转子在
的平面转子在 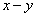 平面上转动,如在
平面上转动,如在  方向加一均匀弱电场
方向加一均匀弱电场 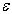 ,求转子的能量至二级修正及基态波函数的一级近似。
,求转子的能量至二级修正及基态波函数的一级近似。
解:平面转子的哈密顿算符为
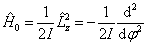 (1)
(1)
已知它的本征解为
 (2)
(2)
显然,除了基态是非简并之外,所有的激发态都是二度简并的。
加上弱电场之后,相当加上一个微扰
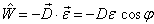 (3)
(3)
对于基态而言,有
 (4)
(4)
这是一个无简并微扰问题,可以直接利用微扰论的公式进行逐级计算。
能量的零级近似与1、2级修正分别为
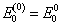 (5)
(5)
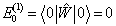 (6)
(6)
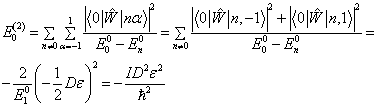 (7)
(7)
波函数的零级近似与1级修正为
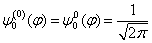 (8)
(8)
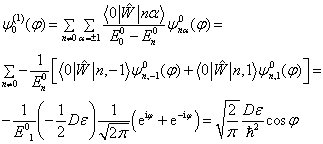 (9)
(9)
对于激发态( 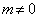 )而言,简并度为2,应该使用简并微扰论进行计算。
)而言,简并度为2,应该使用简并微扰论进行计算。
能量一级修正  应满足久期方程
应满足久期方程
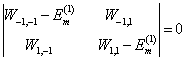 (10)
(10)
其中,
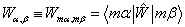 (11)
(11)
由计算可知,算符
 的四个矩阵元皆为零,故能量的一级修正为等于零的二重根,即
的四个矩阵元皆为零,故能量的一级修正为等于零的二重根,即
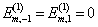 (12)
(12)
欲求能量的二级修正,需要用(9.2.15)式,即
 (13)
(13)
写成久期方程的形式
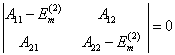 (14)
(14)
式中,
 (15)
(15)
微扰项的矩阵元为
 (16)
(16)
下面分别对 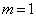 和
和  两种情况进行讨论。
两种情况进行讨论。
当 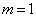 时,久期方程为
时,久期方程为
 (17)
(17)
解之得
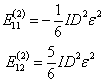 (18)
(18)
能量的二级修正使得第一激发态的简并完全消除。
当
 时,久期方程为
时,久期方程为
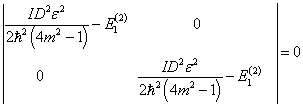 (19)
(19)
显然,有
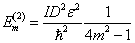 (20)
(20)
例题8.5
设有一个一维非简谐振子,其哈密顿算符为
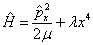
试以线谐振子的本征波函数

为试探波函数,用变分法求其基态能量的近似值。其中, 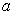 为变分参数。
为变分参数。