例题8.7
一个自旋为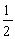 
、磁矩为 
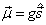的粒子处于如下弱旋转磁场中
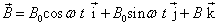
粒子与磁场的作用为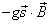 
。若粒子开始处于 
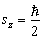的状态，讨论跃迁情况并计算跃迁几率。
解：设粒子所处的初态为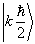 
，末态为 
，
由 
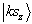到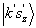 
的跃迁几率振幅为
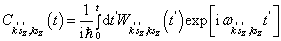（1）
其中，
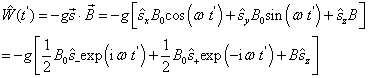（2）
由于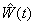 
只与自旋变量有关，所以它不引起量子数 
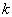的改变。并且，只有（2）式的第一项使得初态变为 
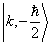，而第三项只能使能级产生移动。其跃迁几率为
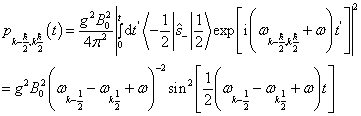（3）
而
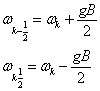（4）
将上式代入（3）式，得到
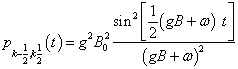（5）
例题8.8宽为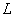 
的一维无限深势阱内有两个质量均为 
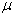的无自旋的粒子，其相互作用势为
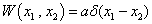，计算基态能量，精确到 
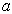的一次项。
解：先不考虑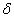 
势，则二粒子在无限深势阱
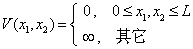
中运动，其哈密顿为
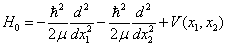
据无限深势阱结果，有
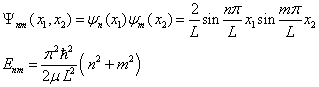
基态，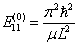 
考虑
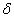势，基态能量修正到一级近似，
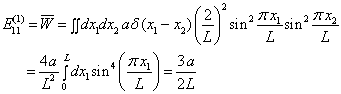
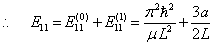
例题8.9求线性谐振子偶极跃迁的选择定则。
解：在只考虑电场作用，即，偶极近似的情况下，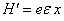 
。跃迁几率
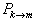与矩阵元
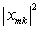成正比。
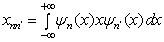
在线性谐振子的情况下，利用
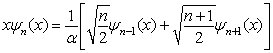
得
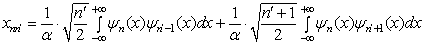
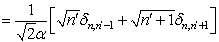
可见，要使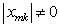 
，必须
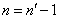或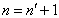 
由此得
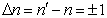
此即线性谐振子偶极跃迁的选择定则。