§8.4.2
线性变分法
试探波函数可以只有一个变分参数,也可以有多个变分参数。若将试探波函数根据
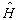 的对称性选成某一组已知函数的线性函数,用其组合系数作为变分参数,则称之为线性变分法,或里兹(Rits)变分法。
的对称性选成某一组已知函数的线性函数,用其组合系数作为变分参数,则称之为线性变分法,或里兹(Rits)变分法。
选
 个尽可能体现
个尽可能体现
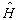 的性质的态矢量
的性质的态矢量
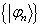 ,它们可能既不正交也不归一,将它们的线性组合成试探波函数
,它们可能既不正交也不归一,将它们的线性组合成试探波函数
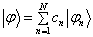 (8.4.28)
(8.4.28)
其中,
 个
个
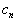 为变分参数。将上式代入哈密顿算符的平均值公式,得到
为变分参数。将上式代入哈密顿算符的平均值公式,得到
 (8.4.29)
(8.4.29)
令
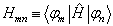 (8.4.30)
(8.4.30)
 (8.4.31)
(8.4.31)
则(8.4.29)变为
 (8.4.32)
(8.4.32)
将上式两端对
 求偏导,注意到,
求偏导,注意到,  取极值的条件
取极值的条件
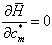 ,有
,有
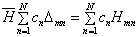 (8.4.33)
(8.4.33)
整理之,得到含有待定参数  的线性方程组
的线性方程组
 (8.4.34)
(8.4.34)
上式有非平庸解的条件是系数行列式为零,即
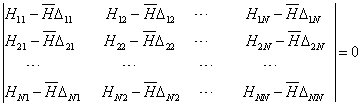 (8.4.35)
(8.4.35)
求解上式可以得到  。一般情况下,
。一般情况下,  有
有
 个值,其中最小者
个值,其中最小者
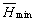 即为基态能量的近似值。为了求出基态波函数,将
即为基态能量的近似值。为了求出基态波函数,将
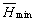 代入(8.4.34)式可以求出
代入(8.4.34)式可以求出
 个
个
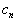 . 将所求得的
. 将所求得的
 个
个
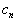 代入(8.4.28),
就求得了基态波函数的近似值。
代入(8.4.28),
就求得了基态波函数的近似值。
应该指出:当构成试探波函数的一组函数是正交的情况下, 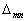 是对角的,而若这组函数是正交归一的,则
是对角的,而若这组函数是正交归一的,则
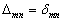 ,这时,(8.4.35)就变成了通常的关于
,这时,(8.4.35)就变成了通常的关于  的久期方程
的久期方程
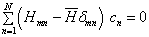 (8.4.36)
(8.4.36)