例题9.2
一个低能粒子受到如下有限深球方势阱的散射
 (1)
(1)
其中, 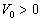 ,且
,且  。用玻恩近似计算总散射截面。
。用玻恩近似计算总散射截面。
解:有所给条件可知,可用玻恩近似计算散射截面。
 (2)
(2)
由此求出微分散射截面
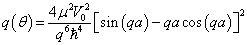 (3)
(3)
在低能情况下, 由于 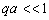 ,故可以将上式中的三角函数作展开,即
,故可以将上式中的三角函数作展开,即
 (4)
(4)
进而得到
(5)
正如预期的一样,微分散射截面与角度 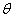 无关,即该截面表现出各向同性的性质。这样,散射的总截面为
无关,即该截面表现出各向同性的性质。这样,散射的总截面为
。
(6)
例题9.3
设一个带电荷 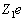 的高速粒子,被一个原子序数为
的高速粒子,被一个原子序数为 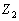 的中性原子散射。当入射粒子距离原子核较远时,核外电子会屏蔽原子核所产生的静电场;而当其非常靠近原子核时,则会感受到全部正电荷的库仑作用。通常用如下的势来描述这种作用
的中性原子散射。当入射粒子距离原子核较远时,核外电子会屏蔽原子核所产生的静电场;而当其非常靠近原子核时,则会感受到全部正电荷的库仑作用。通常用如下的势来描述这种作用
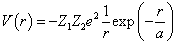 (1)
(1)
其中, 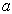 称为屏蔽参数,它的数量级与原子的半径相同。上述相互作用势被称为汤川势。
称为屏蔽参数,它的数量级与原子的半径相同。上述相互作用势被称为汤川势。
将(1)势代入  ,求得微分散射截面
,求得微分散射截面
 (2)
(2)
当  时,汤川势将退化为库仑势,这时,上式变为
时,汤川势将退化为库仑势,这时,上式变为
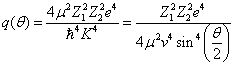 (3)
(3)
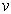 是入射粒子的速度。上述公式与卢瑟福的散射公式完全一样。
是入射粒子的速度。上述公式与卢瑟福的散射公式完全一样。