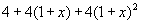
第二步：根据问题的要求和建模目的作出 合理的简化假设。

本例中，我们设增长率为常数 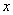。我们说这个假设并不合理，因为实际中的增长率通常不会是常数，但在中学阶段，这个假设就是合理的。换句话说，假设的合理性与研究者所使用的工具和研究范围有关。
    第三步：根据问题分析与假设，利用相应的物理的或其它有关规律建立起现实对象的数学表达式—— 建立数学模型：
    本例经整理后的数学模型是

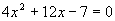
第四步：使用相应的数学方法求解数学模型以给出现实对象的数学解决—— 模型求解

本例使用一元二次方程的因式分解法 (或公式法)解得

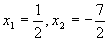
第五步：对模型的解给予检验和解释— 模型分析（包括检验、修改、应用和评价等）

本例中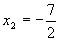，不合实际而舍去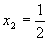，合乎实际而保留，于是现实对象所提问题获得解决。

注意，若所得两解均不符合实际，则所建数学模型有错误，应推倒重建。这是数学建模完全可能出现的情况，其产生原因往往是问题分析错误或假设不合理所至。