1.2.1 数学模型和数学建模

应该说数学模型与数学建模是大家早已十分熟悉的概念。早在中学的时候我们就已经用建立数学模型的方法来解决实际问题了，只不过这些问题是老师为教会学生相关知识而事先人为设置好了的，我们也没有充分注意到它就是数学模型罢了。譬如说下述这类“实际”问题。

设某厂投产一种新型家用轿车，第一年生产了 4 万辆，第二年、第三年产量持续增长，计划到第三年末，市场共拥有 19 万辆这种品牌的轿车，那么后两年的增长率是多少？

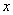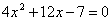这是中学代数中的一道应用题——增长率问题。设平均增长率为 ，则易得。求解之即可。

实际上，这里的一元二次方程就是上述增长率问题的 数学模型。一旦给出这个模型，这个现实问题便转化为纯粹的数学问题，而求解这个数学问题得到的 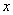的值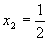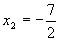， 便给出了这个现实对象的一个解答。当然 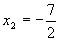经检验不符合题意(实际)而舍去。至此，这个现实对象经过这种数学的处理后获得解决。

诚然，真正实际问题的数学模型与建立数学模型的过程通常要比之复杂得多，但其基本内容与过程已经包含在建立和求解这个代数应用题的过程中了。即有以下建模基本过程：

第一步：根据现实对象的背景和要求进行 问题分析：

若增长率为常数 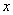，根据题意，第二年的产量为 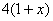，第三年的产量为 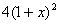，从而到第三年末的总产量为