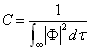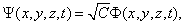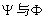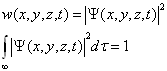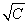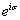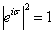2.1 波函数的统计解释

　

    一般情况下，我们用一个函数表示描写粒子的波，并称这个函数为波函数，它是一个复数：

    电子究竟是什么？是粒子？还是波？单个电子就具有波动性。

    粒子性（不是经典的粒子） ：“原子性”或“颗粒性”。

即具有    ,  不与”粒子有确切的轨道“的概念相联系。

　

    波动性（不是经典的波）：波的“叠加性”，并不与某种实际的物理量在空间的分布相联系。

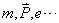
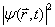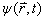
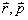
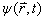
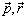
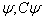    几率波（波动性与粒子性的统一）：波函数的统计解释，玻恩（Born)的波函数的统计解释（1926）波函数在空间中某一点的强度( )和在该点找到粒子的几率成正比。——几率幅，几率波不是机械波，不代表什么实在的物理量的波动，只不过刻划粒子在空间的几率分布而已。

        亮纹：几率大

        暗纹：几率小

　

    量子力学的基本原理之一：微观体系的状态被一个波函数完全描述，从这个波函数可以得出体系的所有性质。波函数一般应满足连续性、有限性和单值性三个条件。

经典力学：状态用 描写。

量子力学：状态用 描写。

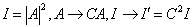
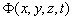
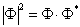
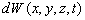     不能同时具有确定值。因为粒子在空间各点出现的几率总和等于1，  描写同一状态，C为常数。

        对于机械波：

                   

　

设描写粒子的状态。

                           

　

表示在时刻t，无限小区域内找到粒子的几率。

　

                    

　

C为比例系数， 体积元。

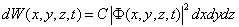
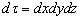
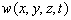
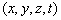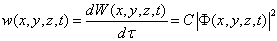
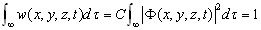
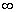表示在时刻t，在点附近单位体积内找到粒子的几率，——几率密度。

　

　

　

表示对整个空间积分。

　

　

若

　

描写同一状态。

　

则

　

归一化常数。

归一化波函数可以含有一个任意相因子  ,