二、全同粒子体系的波函数 泡利原理 1、两个全同粒子体系的波函数 不考虑相互作用时
当第一个粒子处于第 波函数
若将
而能量的本征值仍为
(3)、(5)对应于同一个E的不同的本征函数。E是简并的称交奂简并。
当
且
归一化后
对于两个弗米子,由
如果两粒子间的相互作用不能忽略,则体系的定态波函数
即不能这与成单粒子波函数
2、N个全同粒子体系的波函数
N个全同粒子,无相互作用
|

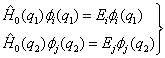 (2)
(2)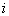 态,第二个粒子处于第
态,第二个粒子处于第 态,体系的能量
态,体系的能量
 (3)
(3) (4)
(4)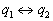 ,则
,则


 时,(
时,(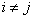 时,即不对称也不反对称。
时,即不对称也不反对称。



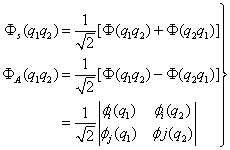 (6)
(6) 描写,当两个弗米子处于同一状态时,即
描写,当两个弗米子处于同一状态时,即 时,由(
时,由( ,即两个弗米子处于同一状态的几率为
,即两个弗米子处于同一状态的几率为

 仍成立。交换简并仍成立,体系的波函数仍可按(
仍成立。交换简并仍成立,体系的波函数仍可按(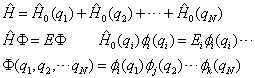

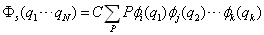

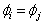 则
则 ,这表明不能有两个或两个以上的全同费米子处于同一状态
,这表明不能有两个或两个以上的全同费米子处于同一状态