| 当前位置:首页<<课程学习<<第七章<<第三节 一元线性回归 | ||
|
第三节 一元线性回归
一、一元线性回归的含义 一元线性回归是指只有一个自变量并且统计量成大体一次函数的线性关系的回归分析。它是回归分析中最简单的部分,但却是进一步学习、理解多元线性回归的基础。对于具有线性关系的两个变量,回归的目的首先是找出因变量(一般即为Y)关于自变量(一般记为X)的定量关系。例如我们用10位大一学生平均每周所花的学习时间及他们期末考试成绩。观察数据我们可以发现两者之间呈正相关,不过更直接的方法是绘制散点图,即分别用两列变量做横、纵轴,描点。若它们的分布在一条带状区域,就预示着两列变量之间有相关。若没有随机误差的影响,这些点将落在一条直线上,这条直线称回归线,它是描述因变量Y关于自变量X关系的最合理的直线。 由于回归关系的不完全确实性,所以我们根据实测数值描绘的散点图,各点不会都在同一条直线上,而是比较分散的。尽管如此,从图上我们还是可以看出,散点图呈线性趋势,而且呈正相关。 二、一元线性回归方程的建立 (一)基本形式 运用代数知识可知直线方程为 Y=a+bX 式中,a是截距,b是斜率。在实际应用中,我们必须首先决定用哪个变量来预测,即要定好X,Y谁是自变量,谁为因变量.用于回归表示的是两个变量单方向的推算关系,所以我们既可以用X去预测Y,也可以用Y去预测X.因此,回归方程有两个。 当我们以X为自变量预测Y时,方程为
式中,斜率b又称为回归系数,是线性回归方程中自变量的系数。有时特指只有一个自变量时线性回归方程中自变量的系数。其意义表示当其他自变量不变时,该自变量变化一个单位时因变量变化的单位数。根据方程即可以由X值对Y值作出估计,从而得到Y的估计值,记为 当我们以Y为自变量预测因变量X时,方程则为
这是由Y估计X的方程,又称X对Y的回归方程。 (二)b和a的求解原则和方法 1.最小二乘法
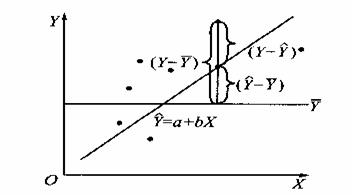
建立一个线性回归方程实际上就是确定一条直线,也就是求公式中的两个常数—截距a和回归系数b,而研究这样一条直线的常用方法是最小二乘法,这种方法需要我们找到这样一条直线,使所有的点到直线的垂直距离的平方和最小,也称最小平方法或最小二乘估计,如图7-2。 (引自张厚粲,徐建平《现代心理与教育统计学》)
2.平均数和标准差计算法
其中,
若 |
||
| ---[1] [2] [3] [4]--- | ||

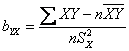
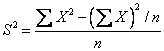
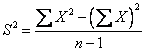 ,则有
,则有