三、回归系数和相关系数的关系

和是一元线性回归样本回归方程的回归系数。，同理，。可见，b与相关系数同号，同样代表相关的方向。同时，联合前两式可得

                                 (7.19)

这说明，相关系数是两个回归系数的几何平均。由此说明了r与b的密切关系。

首先，二者是密切联系的。线性回归与相关系数的计算收拾以两个连续变量的共变数为基础，其基础原理相似。

其次，二者又有明显的不同。回归分析是用一个变量去预测另一个变量的变化情形，往往是单向地分析两变量的变化关系，x与y各自有着不同的地位和作用，因此回归分析是一种不对称设计。但计算相关系数时，考虑的是两个变量的变化情况，相关表示两方面的平均关系，属于对称性设计，因此相关分析是双向的，不强调哪个是自变量、哪个是因变量。

四、一元线性回归的检验

1.回归方程的有效性检验

如前所述，不管两个变量之间是否存在线性相关关系，只要有两列数据，一般都可以建立起一个回归方程。但根据样本数据得出的回归方程是否真正反映了两个变量之间的线性关系，或者说自变量是否真的对因变量有影响，用它来预测或估计的有效程度如何，是应用回归方程时必须解决的问题。因此，建立了回归方程后，还要对它进行检验和评价。

对回归方程有效性的检验有三种方法。

第一种检验方法是对一元线性回归方程进行方差分析。

第二种检验方法是对两个变量相关系数进行与总体零相关显著性检验。如果两个变量之间相关程度比较显著，那么根据回归方程对因变量的估计和预测的可靠性程度就比较高；如果两个变量之间的相关程度比较低或几乎不相关，那么就无法对因变量进行估计和预测，也就失去了回归的意义。所以，两个变量之间有显著性相关，是保证对因变量估计和预测的可靠性程度的前提条件。

第三种检验方法是对一元线性回归方程中的回归系数进行显著性检验。检验时，只需对由x估计y或由y估计x中的一个回归方程的回归系数进行检验即可。

（1）一元线性回归方程方差分析检验步骤。

第一步，对总变异进行分解

总离差平方和;                 (7.20)

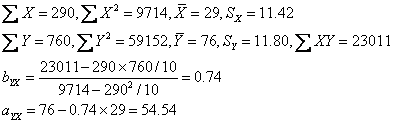
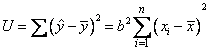回归平方和，即完全由自变量x所决定的变异；                                     (7.21)

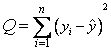剩余平方和，即不确定部分所决定的变异。                                               (7.22)

                                                                                                   (7.23)

第二步，给定显著性水平，根据F检验表，查得自由度为的临界值。

第三步，进行F检验，作出统计决断。