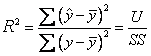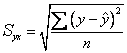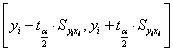当前位置:首页<<课程学习<<第七章<<第三节 一元线性回归

（1）对两个变量的相关系数进行显著性检验的步骤。

第一步，按公式计算出相关系数r的值。

第二步，给定显著性水平，根据相关系数检验表，查得自由度为n-2的临界值。

第三步，若,表明变量x与y之间存在的线性相关关系显著，回归效果也显著。若,表明变量x与y之间存在的线性相关关系不显著，或者变量x与y之间不存在线性相关关系，回归的效果也就不显著。

（2）           回归系数的检验步骤

样本回归系数的抽样分布呈t分布，其检验统计量为

                 (7.24)

第一步，提出假设。

第二步，计算统计量t。

第三步，给定显著性水平，根据t值表，查得自由度为n-2的临界值。

第四步，进行t检验，作出统计决断。

2.回归方程有效性指标——测定系数

回归方程经检验有显著性，只是说明其与无效的回归方程相比，二者是有统计学意义的差异的。但到底有效性高到什么程度，估计和预测的效果如何，还尚无从得知。因此，必须求解衡量回归方程有效性高低的指标，才能回答这个问题。测定系数就是这样一个指标，记作,求解公式为

                           (7.25)

从上式中可以看出，测定系数即回归平方和U在总平方和SS中所占的比例，也就是自变量对于因变量变化的预测力。比如，=0.70,表明变量y的变异中有70%是由变量x的变异引起的，或者说有70%的变异可以由x的变异解释。因此，测定系数数值越大，表明回归方程越有效、预测效果越好。

五、一元线性回归方程的应用

建立回归方程的最终目的是利用方程从已知事实推测相应的未知事实，即进行预测。预测是将已知变量值作为自变量代入相应的回归方程而推算出另一个变量的估计值及置信区间统计方法。如上例中，已知某个学生的学习时间为35小时，由此推算出其测验成绩的估计值为

但是，其实际成绩很可能并不正好等于预测值，而会在这一数值上下波动，即会在一个区间范围内波动，这个区间范围的大小与预测误差的大小有关。

1.用样本回归方程推算回归值

对于一个已经建立好的有效的样本回归方程，如果要利用该回归方程对样本中某一个体自变量x所对应的因变量值进行预测，即是对回归值的预测，可以直接代入样本回归方程求解，所得结果即的点估计值。会围绕上下波动。波动的标准误为

或

                          (7.26)

即针对某一样本而言的误差的标准差。

因此，置信区间为1-时，对于确定的x值，回归值的置信区间为                                                          (7.27)

当样本容量较大时，可以用正态分布的代替。

2.对回归主值的点估计与区间估计
---[1] [2] [3] [4]---