|
设晶体中第 m
个原子的位矢为:
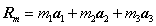 ……………………………………………………………………………(5-4-1) ……………………………………………………………………………(5-4-1)
若将该原子看作一个孤立原子,则在其附近运动的电子将处于原子的某束缚态  ,该波函数满足方程: ,该波函数满足方程:
 ………………………………………………( 5-4-2) ………………………………………………( 5-4-2)
其中  为上述第 m 个原子的原子势场, 为上述第 m 个原子的原子势场,
 是与束缚态 是与束缚态  相对应的原子能级。如果晶体为 N个相同的原子构成的布喇菲格子,则在各原子附近将有 N 个相同能量 相对应的原子能级。如果晶体为 N个相同的原子构成的布喇菲格子,则在各原子附近将有 N 个相同能量  的束缚态波函数 的束缚态波函数  。因此不考虑原子之间相互作用的条件下,晶体中的这些电子构成一个 N 个简并的系统:能量为 。因此不考虑原子之间相互作用的条件下,晶体中的这些电子构成一个 N 个简并的系统:能量为  的 N 度简并态 的 N 度简并态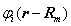 , m=1 , 2 ,…, N
。 , m=1 , 2 ,…, N
。
实际晶体中的原子并不是真正孤立、完全不受其它原子影响的。由于晶体中其它诸原子势场的微扰,系统的简并状态将消除,而形成由 N 个能级构成的能带。根据以上的分析和量子力学的微扰理论,我们可以取上述 N 个简并态的线性组合
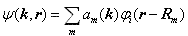 ………………………………………………………………………( 5-4-3) ………………………………………………………………………( 5-4-3)
作为晶体电子共有化运动的波函数,同时把原子间的相互影响当作周期势场的微扰项,于是晶体中电子的薛定谔方程为:
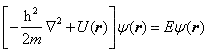 …………………………………………………………………( 5-4-4) …………………………………………………………………( 5-4-4)
其中晶体势场 U ( r )
是由原子势场构成的,即
 …………………………………………………………………( 5-4-5) …………………………………………………………………( 5-4-5)
|

