|
1,自由电子模型。 这个模型首先由特鲁德提出来。他假设金属价电子是在金属内的恒定势场中彼此独立地运动的。这个模型忽略了电子和离子实以及电子和电子之间的相互作用。
经典的自由电子模型假定:在热平衡时,电子速度服从麦克斯韦—玻耳兹曼统计律。这个模型虽然因能够推导出魏德曼—弗兰兹定律而得到承认,但这个模型却不能解释为什么电子气对晶体总热容的贡献极小这样一个实验事实和其它一些实验事实。
量子电子气模型认为电子服从费米分布.这个模型可以得到电子气热容贡献极小的结论。但不能解释在高纯晶体中电子的平均自由程极大的事实,也不能解释为什么晶体会有导体、绝缘体及半导体。
2 、费米能 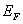 。 。 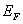 是费米分布函数中的一个参量,具有能量的量纲,其数值由电子总数来确定。费米能实际上是系统中电子的化学势。 是费米分布函数中的一个参量,具有能量的量纲,其数值由电子总数来确定。费米能实际上是系统中电子的化学势。
在 T=0K 时,费米能 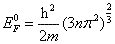
在 T=0K 时,费米能 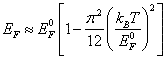
可见, 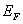 与 与 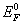 的数值相近, 的数值相近, 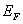 随温度升高而略有下降。 随温度升高而略有下降。 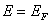 的等能面称作费米面。在自由电子模型中,费米面是球面,球半径为 的等能面称作费米面。在自由电子模型中,费米面是球面,球半径为 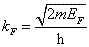 。在 T = 0K 时,低于费米能级和所有状态均为电子所占据,高于费米能级的所有状态全部空着。即在绝对零度下,费米能级是被电子占据的状态与未被电子占据的状态的分界面。如果不是绝对零度,高于费米能级的状态也可能有电子,低于费米能级的状态也可能空着。 。在 T = 0K 时,低于费米能级和所有状态均为电子所占据,高于费米能级的所有状态全部空着。即在绝对零度下,费米能级是被电子占据的状态与未被电子占据的状态的分界面。如果不是绝对零度,高于费米能级的状态也可能有电子,低于费米能级的状态也可能空着。
3 、电子比热容和金属的比热容。 若系统中共有 N 个电子,则得到低温下电子的比热容为:
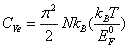
即电子的比热容与温度成正比。这个比热容比经典给出的比热容小得多。金属的比热容由两部分组成,即晶格的比热容和电子的比热容。在低温下,金属的比热容为
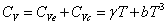
4 、布洛赫定理。 在绝热近似、单电子近似和周期场近似下,电子可以视为在周期场中运动,其电子波函数满足
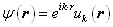
其中 u ( r ) 具有晶格周期性。上述结论称为布洛赫( Bloch )定理。
5 、近自由电子模型。 这个模型假设晶格势场中周期变化的部分是很弱的,可以作为微扰来处理。以自由电子的解作为零级近似,考虑了波函数的一级修正及能量的二级修正后,得到晶体电子的波函数
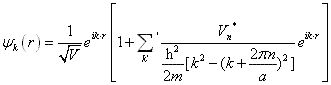
具有布洛赫波的形式;电子能量为
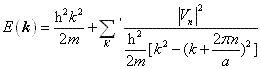
当电子的波矢 k 满足 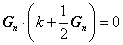 时,电子能量 E( k ) 发生分裂,成为 时,电子能量 E( k ) 发生分裂,成为
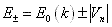
|

