|
能隙 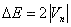 的范围内,不存在电子的能量状态,称之为禁带,禁带宽度是 的范围内,不存在电子的能量状态,称之为禁带,禁带宽度是 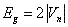 , , 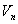 是晶格周期场的傅氏展开系数,周期场愈强, 是晶格周期场的傅氏展开系数,周期场愈强, 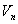 愈大,因而禁带愈宽。 愈大,因而禁带愈宽。
晶体电子的能量 E( k ) 是倒格子空间的周期函数,即
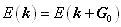
而且有: 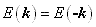
6 、紧束缚模型。 该模型假设晶体势场较强,当电子在 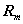 处离子实附近时,主要受该离子实势场的影响,其它离子实对这个电子的影响很小,可以作为微优处理。以孤立原子的哈密顿算符作为零级近似,应用简并微扰论进行计算,结果表明,晶体电子的能量本征值是一系列能带,其表达式为 处离子实附近时,主要受该离子实势场的影响,其它离子实对这个电子的影响很小,可以作为微优处理。以孤立原子的哈密顿算符作为零级近似,应用简并微扰论进行计算,结果表明,晶体电子的能量本征值是一系列能带,其表达式为
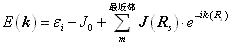
其中 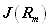 是最近邻原子间的微扰矩阵元,其量值与最近邻原子间波函数的交叠有关,波函数的交叠越大,则能带宽度越大。 是最近邻原子间的微扰矩阵元,其量值与最近邻原子间波函数的交叠有关,波函数的交叠越大,则能带宽度越大。
7 、能态密度 N ( E )。 N(E)=d z /dE ,表示能量在 E 与 E+dE 之间的单位能量间隔中所含有的状态数。自由电子模型中, N ( E )随 E 增大而增大,其表达式为:
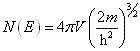
晶体中电子的等能面较复杂,不易得到其具体表达式
8 、准经典近似。 用经典概念描述晶体中布洛赫电子有时会带来某些方便。引入经典概念后,得到:
晶体电子的准动量为: 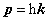
晶体电子的速度: 
晶体电子倒有效质量张量: 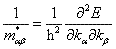
有效质量与能带结构密切相关,随 k 的变化而变。在能带底,有效质量是正的;在能带顶,有效质量是负的。有效质量的各种特性是由于它概括了周期场对电子的作用,使电子的加速度与外力直接联系起来,所以,与电子的惯性质量是截然不同的,在窄的能带中,电子的有效质量大,反映了该带电子受周期场的作用强,公有化运动较弱;宽能带电子的有效质量较小,故公有化运动较强。
9 、空穴。 空穴是为了便于研究近满带电子行为而引人的概念.空穴是一种假想的粒子,这种粒子带正电荷,具有正的有效质量 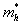 ,运动速度与 k 态电子相同。空穴的实质是近满带顶附近空的能量状态,即 k 态不为电子占据,则存在一个空穴。空穴运动的实质是电子的运动。 ,运动速度与 k 态电子相同。空穴的实质是近满带顶附近空的能量状态,即 k 态不为电子占据,则存在一个空穴。空穴运动的实质是电子的运动。
10 、导体、绝缘体及半导体晶体的能带模型。 由于晶体中电子能量是 k 的偶函数,电子的速度必为 k 的奇函数,所以满带电子不导电,不满带电子才导电。对于导体,晶体能带中除了满带外,还有不满带,其价电子能带是不满带。对于绝缘体,晶体能带中除了满带外.就是空带,而且,最高的满带与最低的空带之间的禁带宽度较大,约大于 5ev ;对于半导体材料,与绝缘体的模型无本质差异,只是最高满带与最低空带之间的禁带宽度较窄, 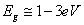 。所以,在 T = 0K 时,半导体是个绝缘休; T≠ 0 时,满带电子有少量被热激发到上面的空带中,而在满带留下少量的空穴,因而具有一定的导电性。 。所以,在 T = 0K 时,半导体是个绝缘休; T≠ 0 时,满带电子有少量被热激发到上面的空带中,而在满带留下少量的空穴,因而具有一定的导电性。 |

