|
尽管所有的固体都包含大量有电子,但有些固体具有很好的电子导电性能,而另一些固体则观察不到任何电子的导电性。对于固体为什么分为导体、绝缘体和半导体呢?这一基础事实曾长期得不到解释,能带论对这一问题给出了一个理论说明,并由此逐步发展成为有关导体、绝缘体和半导体的现代理论。
晶体中电子有能量本征值分裂成一系列能带,每个能带均由 N 个准连续能级组成( N 为晶体原胞数),所以,每个能带可容纳 2N 个电子。晶体电子从最低能级开始填充,被电子填满的能带称作满带,被电子部分填充的能带称为不满带,没有电子填充的能带称为空带。能带论解释固体导电的基本观点是:满带电子不导电,而不满带中的电子对导电有贡献。
5.6.1 满带电子不导电
从前面的知识中,已经知道,晶体中电子能量本征值 E ( k )
是 k 的偶函数,则利用(5-5-11),可以证明 v (-
k)=- v ( k ) ,即 v (
k ) 是 k 的奇函数。一个完全填满的电子能带,电子在能带上的分布,在 k
空间具有中心对称性,即一个电子处于 k 态,其能量为 E(
k ) ,则必有另一个与其能量相同的 E (-
k )= E ( k ) 电子处于 -
k 态。当不存在外电场时,尽管对于每一个电子来证,都带有一定的电流 -e v
,但是 k 态和 - k
态的电子电流 - e v ( k ) 和 - e
v (- k )正好一对对相互抵消,所以说没有宏观电流。
当存在外电场或外磁场时,电子在能带中分布具有 k
空间中心对称性的情况仍不会改变。以一维能带为例,图5-6-1中 k
轴上的点子表示简约布里渊区内均匀分布的各量子态的电子。如上所述,在外电场 E
的作用下,所有电子所处的状态都以速度
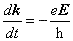 ………………………………………………………………………………(5-6-1) ………………………………………………………………………………(5-6-1)
沿 k
轴移动。由于布里渊区边界 A
和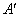 两点实际上代表同一状态,在电子填满布里渊区所有状态即满带情况下,从 A
点称动出去的电子同时就从 两点实际上代表同一状态,在电子填满布里渊区所有状态即满带情况下,从 A
点称动出去的电子同时就从 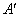 点流进来,因而整个能带仍处于均匀分布填满状态,并不产生电流。 点流进来,因而整个能带仍处于均匀分布填满状态,并不产生电流。 |

