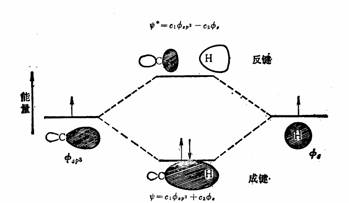
S轨道和SP³杂化轨道组成的分子轨道

P轨道可以头对头组合成σ分子轨道，也可以肩并肩交盖而组合成π分子轨道。

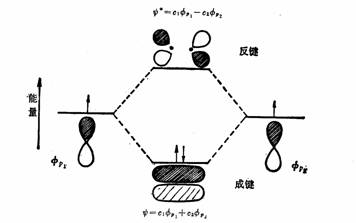
P轨道组合成π分子轨道

由一对自旋反平行的电子占有分子轨道构成的键是双电子键，由一个单电子占有分子轨道构成的键叫单电子键，如氧分子的成键情况就含有单电子π键。这从价键理论不好解释，而按分子轨道理论是很容易理解的。如下图所示，余下的两个电子，根据洪特规则只能分别填充到两个简并的π^*轨道上，而且是自旋平行的，因此氧分子表现为顺磁性。

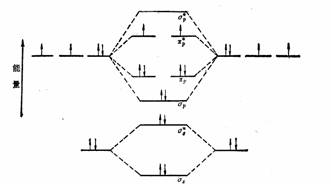
氧的分子轨道

2．休克尔（Hǔckel）分子轨道法

通过薛定谔方程求解分子轨道系数和计算轨道能量是非常复杂的，一般只采用近似的方法进行处理。其中比较简单、也是在描述π电子体系时经常用到的近似法就是休克尔分子轨道法，简称为HMO法。

利用休克尔分子轨道法近似求解薛定谔方程，可以得到分子中π电子体系的总能量，个别分子轨道的能量和分子轨道线性组合中原子轨道函数的系数。在此我们不讨论一系列的数学计算，主要介绍其结论和应用。

如乙烯分子中碳原子以SP²杂化成键，构成五个σ键，这些σ键组成共平面骨架，而π体系的P轨道组合为两个分子轨道：

ψ=c₁φ₁+c₂φ₂

 ψ^*= c₁φ₁-c₂φ₂

以α代表碳原子2P轨道的能量，以β表示相邻原子轨道相互作用的能量（由于考虑的只是SP²杂化碳原子P轨道构成的π体系，α和β可近似视为常数），采用休克尔分子轨道法近似计算，成键轨道ψ能量为α+β，而反键轨道ψ^※的能量α-β，在基态时，两个P电子在成键轨道，总能量E=2(α+β)。

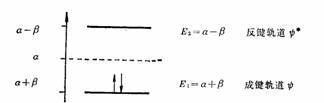
因为 P电子的能量为α，π键的键能可以简单地计算为：

E_π=2(α+β)-2α=2β

 对于1，3-丁二烯，根据HMO法计算，四个2P轨道线性组合四个分子轨道，其能量计算为：

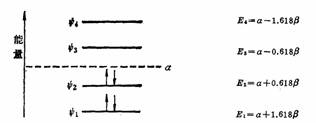
    基态时地总能量  

    E=2E₁+2E₂=2(α+1.618β)+2(α+0.618β)=4α+4.472β

    如果按两个孤立π键计算，总能量应为4α+4β（乙烯的两倍），两者相差0.472β，这个能量是1，3-丁二烯特殊的稳定能，是由于电子离域的结果，称为离域能或共轭能。

共 6 页 1 2 3 4 5 6