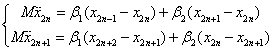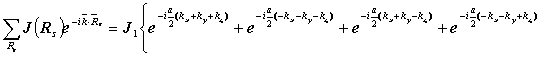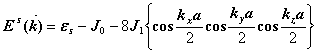综合模拟题二（答案）

一、填空（ 15 分）

1 、原胞是指 (晶体中体积最小的周期结构单元) 。

2 、在倒格子空间中，一个倒格点代表正格子空间中的 (一族晶面 )。

3 、晶体学中考虑到对称性，将晶体结构划分为( 七 )个晶系，( 十四 )种布拉伐格子。

4 、极化激元是 ( 离子 )晶体中，光子与( 横向光学声子模) 的耦合量子。

4 、当光与 ( 声学波 )相互作用时，称为布里渊散射；当光与( 光学波 )相互作用时，称为喇曼散射。

5 、一维复式格子中，长光学波代表( 原胞内不同原子的相对振动) , 而长声学波代表 (原胞质心的振动 )。

6 、 空间中能量等于 E F 的等能面称为 (费米面) ，即在绝对零度时，是 (电子占有) 与 (不占有) 区域的分界面。

7 、晶体中电子的有效质量不仅可以取正值，也可以取负值，一般在 能带底附近的有效质量总是正的，而在(能带顶)附近的有效质量总是负的。

8 、 典型的热缺陷有 (肖脱基缺陷) 和 (夫伦克尔缺陷 )。

二、证明题（ 3 × 15 分）

(1) 对于简立方晶格，证明密勒指数为 ( h,k,l )的晶面系，面间距d为：，其中a为立方边长。

解：简立方晶格原胞基矢： ；

倒格子基矢为：

对于 (hkl)晶面系有：

对应的面间距为：

所以求得：

(2)设格波的色散关系为 ,求证：二维情况下的频率分布函数为 （S为二维晶格的面积）。

解：二维波矢空间内，格波的等频线是一个个圆周，在 q~q+dq范围内的格波数目 ；

由 可得 ；

所以

证明：一维金属中自由电子的能态密度为： （L为晶格长度）。

解：自由电子的色散关系为：

则

k空间中E与E+dE之间的范围

该范围内的状态数

所以

三、计算题（ 2×20 分）

1、 对于线性链有机化合物 ...CH ＝ CH － CH ＝CH ... ，设 CH 基的质量为 M ，单键与双键处的力常数分别为 β 1 和 β 2 ：

（ 1）写出运动方程；

（ 2）证明色散关系如下：

（ 3）试绘出 β 1 < β 2 时的色散曲线，并分析当 β 1 与 β 2 趋于相等时晶格振动情况。

解：    ...CH ＝ CH － CH ＝CH ... 

原子序号: 2n-1   2n   2n+1  2n+2

运动方程：

若色散关系为 （ β 1 < β 2 ）

分析：；当 β ₁ < β ₂ = β 时，

讨论：此时不再是简单的单键或双键，而是变成一种混合键，若把 CH看成一个原子，则晶体看成简单格子，其晶格常数为 a /2,中心布里渊区为（ ）；若看成复式晶格结构，则晶格常数仍为 a , 中心布里渊区为（ ），由晶格振动的周期性可知， ω + 可等价看作是（ ）和（ ）区域内的光学支，而 ω - 即是声学支。

2、用紧束缚近似理论计算体心立方晶格的s态原子能级相对应的能带函数 E ^s ()（只计最近邻的相互作用），并证明在带底附近等能面近似为球面。

解：（ 1）由紧束缚近似理论知：

对于体心立方晶格，最近邻数为 8，且 = J 1

分别为：

则有

所以，

（ 2）当 时，有

对其它同类项作同样处理后，得到：

取一级近似，忽略高次交叉项，得到：

可见， E(k)与k的方向无关，即等能面为球面。