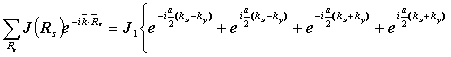综合模拟题三 答案 一、选择题( 3×8=24 分) 1 、晶体中体积最小的结构单元称为( A )。 A .原胞 B .晶胞 C .布里渊区 D .布拉伐格子 2 、晶体结合方式中,电子云形状没有发生根本性改变的是( D )。 A .金属晶体 B .离子晶体 C .分子晶体 D .范德瓦尔斯结合 3 、下列物质中,晶体结构属于简单晶格的是( C ) A . NaCl B . Si C . Cu D . ZnS 4 、光与( )相互作用时,称喇曼散射;当光与( )相互作用时,称布里渊区散射。正确答案是( B ) A .格波 声子 B .光学波 声学波 C .声子 光学波 D .格波 极化激元 5 、设面心立方结构晶格常数为 a ,则最近邻和次近邻原子间距为( B )。 A . a ,
a B . 6 、设倒格子矢量 A .垂直 B .平行 C .成 30 度角 D .成 60 度角 7 、设晶体结构中正格子原胞的体积为 V C ,则其倒格子原胞的体积为( A ) A . 8 、晶格原胞的基矢 A .不唯一,唯一,唯一 B .不唯一,不唯一,唯一 C .唯一,不唯一,唯一 D .唯一,不唯一,不唯一 二、简单回答题( 3 × 4=12 分) 1 、说明波矢空间与倒格子空间的关系。 波矢空间与倒格子空间处于统一空间,倒格子空间的基矢分别为
空间中一个倒格点对应体积的 1/N ,由于数目 N 很大,一个波矢点对应的体积与一个倒格点体积相比甚小,故波矢点在倒格空间是极 为稠密的。因此,在波矢空间内作求和处理时,其内的状态点可看成是准连续的。 2 、说明一维双原子晶格振动的光学支和声学支的本质区别。 长光学支格波的本质是每个原胞内的不同原子做相对振动,振动频率较高,包含了晶格振动频率最高的振动模式;长声学支的本质 是原胞内不同原子没有相对位移,原胞质心的振动,振动频率较低,包含晶格振动频率最低的振动模式,波速是一常数。任何晶体都存 在声学支格波,但简单晶格(非复式晶格)晶体中不存在光学支格波。 3 、 试用能带论解释导体、半导体和绝缘体的区别。 晶体电子的状态由原分立的原子能级分裂为能带,电子填充能带的情况分为满带、不满带和空带,对于半导体和绝缘体,只存在满 带和空带,最高的满带称价带,最低的空带称导带,导带与价带之间的间隔称带隙,一般绝缘体的带隙较大,可达 10ev ,而半导体的 带隙较小,只有 1ev ;对于导体,除满带和空带外,还存在不满带,即导带是不满带。满带电子不导电,而不满带中的电子参予导电, 半导体由于带隙较小,价带电子受到激发后可以跃迁至导带而参予导电,绝缘体的带隙较大,价带电子需获得很大能量才能激发,故一 般情况下,不易产生跃迁现象。 三、计算证明题( 64 分) 1 、( 10 分) 证明两种一价离子组成的一维晶格的马德隆常数为: α =2ln2 证明:如右图所示: ……+ - + - + -……
由于
所以 α =2ln2 2 、( 16 分) 若已知三维晶格的模式密度为
解:频率为 ω 的零点振动能为
故晶格总的零点振动能为
其中已知: 其中由
由于
3 、( 18 分) 证明:二维金属中自由电子的能态密度为:
解:对于二维情况:
其中
所以,
4 、( 20 分) 用紧束缚近似理论计算面心立方晶格的 s态原子能级相对应的能带函数Es(
球面。 解:( 1)由紧束缚近似理论知:
对于面心立方晶格,最近邻数为 12,且
则有
所以,
( 2)当
对其它同类项作同样处理后,得到:
取一级近似,忽略高次交叉项,得到:
|
版权所有:东北师范大学网络教育学院 |
||||
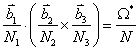 ,即波矢空间中一个波矢点对应的体积是倒格子
,即波矢空间中一个波矢点对应的体积是倒格子 ;
;