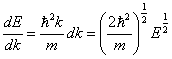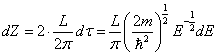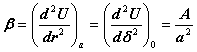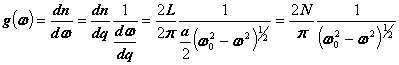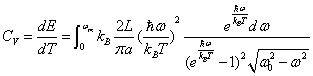综合模拟四 答案 一、请解释下列概念( 6×5=30分) 声子,布里渊区,布洛赫波,有效质量,晶格振动,倒格子 1 、
声子 是指晶格振动的能量量子,能量为
2 、 布里渊区 是指在一个晶格的倒格子空间中,以某一点为原点,作所有倒格矢的垂直平分面,围成的一个个封闭多面体称为布里渊区,从内向外分别为第一布里渊区,第二布里渊区等等。布里渊区即为倒格子空间中的维格纳 - 赛兹原胞。 3 、 布洛赫波 是指 晶体中的电子处在晶格周期性势场中,其波函数受到晶格周期性势场的调制,即晶体中的电子波可认为是一种被周 期性势场调制了振幅的平面波,称为布洛赫波。 4 、 布洛赫电子的 有效质量 m*是晶体中电子准经典运动的加速度对外力的响应,包括了晶格周期场的作用,一般说来,沿不同方向 mx*,my*,mz* 不一定相等,加速度与外力方向可以不同 ; 而惯性质量是经典运动的粒子的加速度对外力的响应。 5 、 晶格振动 是晶体中的原子围绕其平衡位置作微小振动的一种振动方式。 6 、 倒格子 , 又称“倒易点阵”,是从晶格周期性出发,为使固体内各种过程和现象作理论分析时大为简化而引入的概念。设晶格的 三个基矢为
矢”,构成的空间结构称为倒格子。 二、计算证明题( 70 分) 1 、( 10 分)若考虑到次近邻相互作用,求二维正方结构的马德隆常数。 答:计算公式为:
2 、( 10 分)如果将等体积的球堆积成简立方结构,则刚球所占体积与总体积之比是多少? 答:在一个简立方晶格中,刚球所占体积为
3 、( 15 分) 证明: T=0K时,自由电子的费米能级为
解:自由电子的能量本征值为
自由电子能态密度为
由费米能级的物理意义可得
这里令
则可得
4 、( 20 分) 证明:一维金属中自由电子的能态密度为:
解:自由电子的色散关系为:
则
k空间中E与E+dE之间的范围
该范围内的状态数
所以
5 、( 25 分) 设一长度为 L的一维简单元晶格,原子质量为m,间距为a,原子间的互作用势可表示为
(1)色散关系; (2) 模式密度 g(ω); (3)用德拜模型的思想求晶格热容(只列出积分表达式即可)。 解:( 1)原子间弹性恢复力系数:
已知一维单原子链的色散关系是
所以,
( 2)设振动模式数为原子总数N,q的分布密度为L/2 π , 则 dq 范围内的振动模式数为
( 3)频率为ω的格波的热振动能为
整个晶格热振动能为
则比热为
|
版权所有:东北师范大学网络教育学院 |
||||
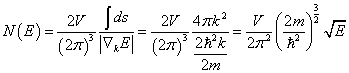
 (L为晶格长度)。
(L为晶格长度)。