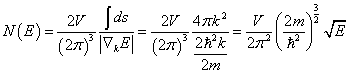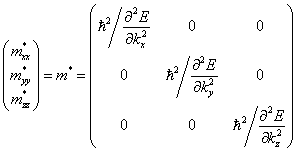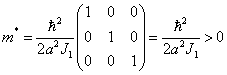综合模拟五 一、填空题 ( 5×3=15分) 1 、重要的化合物半导体 Ge , Si 以及灰锡等都具有(金刚石)结构,这是(复式)晶格,属于(立方)晶系,配位数为(4)。 2 、体心立方结构中晶格常数为 a ,则最近邻格点的间距为(
3 、密堆积结构包括( 六角密排 )和( 面心立方结构 )。 4 、负电性数值大表明吸引电子能力( 强 )。 5 、如果将等体积的球堆积成简立方结构,则刚球所占体积与总体积之比是( 0.52 )。 二、解释概念题 ( 4×5=20分) 原胞:是指晶体的周期性结构中最小的结构单元. 色心:色心是指离子晶体中尤其是碱金属卤化物晶体中 , 由于离子空位陷住电子或空穴 , 使原为透明的晶体出现颜色 , 这种缺陷中 心称为色心 , 有 F 心和 V 心 色散关系:格波的频率 ω 与格波波矢的关系 ω ( q )称为晶格振动的色散关系. 费米面:指 T=0K 时, k 空间占有电子与不占有电子区域的分界面,费米面的能量值为费米能级,动量
三、计算证明题 ( 3×14=42 分) 1 、如果将等半径(半径为R)的圆球球堆积成面心立方结构(晶格常数为 a )设圆球所占体积与总体积之比为 X ,请计算 X 值? 解:如图所示,有下列方程:
可得
2 、一维单原子链,晶格常数为 a ,力常数为 β ,请计算简谐近似下,只考虑最近邻情况下的晶格振动色散关系. 解:设 x n
表示第 n 个原子的位置,则运动方程为:
设试探解为: 3 、 证明:三维情况的金属中自由电子的能态密度为:
证明: 自由电子的能量本征值:
四、综合题 ( 23 分) 用紧束缚近似理论计算简单立方晶格的 s态原子能级相对应的能带函数E
s( 有效质量。 解: (1)公式:
令
可得:
化简:
(2) 公式:
代入计算得:
( A )能带底, k =(0,0,0) :
( B )能带顶,
|
版权所有:东北师范大学网络教育学院 |
||||
 ,则
,则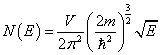 ( V 为晶体体积).
( V 为晶体体积).