1.3.3 求解数学模型

有了数学模型，只要它是可解的，总可以设法利用我们所掌握的相应的数学工具给予求解。请注意：在求解之前，往往还有一个简化模型的前期工作，这要依据模型结果是否容易运用和进一步分析推广等因素来具体决定。

例 1“方桌问题”数学模型的求解   本问题模型

“方桌问题”模型的求解实际上是要证明一个函数的零点存在性，只须构造一个适当的辅助函数，然后利用连续函数的介质定理的特例，即零点定理予以证明即可，这个证明留给学员。

例 2“走步问题”模型的求解   本问题模型

由于求的是 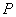的最小值，因此可利用导数方法，即令 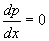便可求得最佳步长及步数

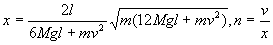
例 3“热传导问题”模型的求解   本问题模型

我们的目的是对两种玻璃窗的效果进行比较，而这只须将两个不同的热传导值进行比较即可。明显地有
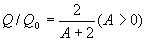                                                        (1.8)