数学的表现形式具有抽象性,但数学所反映的内容又是非常现实的。学习数学的过程不只是让学生记住数学事实,还应当让学生形成数学意识,建立数感。了解数学的价值,认识数学与生活的密切联系。为学生提供具体的问题情境,让学生
如,认识20以内的数时,让学生说一说自己身边的数。学生可能不局限于当前所学的数,他们说出来的数也会有许多超出当前的学习内容。但在这个过程中,学生将体会到,课堂中所学的数在他们身边,他们所遇到的这些都会在数学中学习。下面是新教材中的一个插图,学生借此可能会想到许多自己身边的数。

认识小数时,让学生到超级市场或附近的商店观察各种物品的价格。把这些价格写下来,到班级来交流,说一说看到了什么,为什么要这样写,不同的数表示什么意思。为什么不能都用整数表示?学生在这个过程中有自己的探索,有同学之间的交流,有对小数的具体感知。
以往的计算过多地注重形式化,单纯的“式题”过多。学生很少了解为什么要进行这样的计算。不知道在具体情境下选择什么样的计算方法。计算教学的改革首先要认识计算在数学教育中的作用。计算是帮助我们解决问题的工具,在具体的情境中才能真正认识计算的作用。把计算放在现实的情境中,让学生了解为什么要计算,选择什么方法进行计算,学生就会将计算作为解题的一个组成部分,把计算与实际问题情境联系起来。美国《学校数学课程与评价标准》中对计算问题有一段论述,反映了对计算在数学教育中的价值,以及计算与实际问题之间的关系(见下图)。
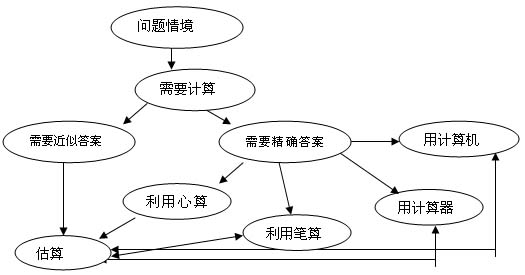
从上面关系图可以了解到,计算是解决数学问题的一个组成部分,计算的价值与具体的问题情境有关。在解决数学问题时,首先应当理解具体的情境的意义,确定是否需要计算;然后再确定需要什么样的计算方法,口算、笔算、计算器、计算机和估算都是供学生选择的方式,都可以起到算出结果的目的。在这里计算方法的重要程度,取决于具体情境的要求。如,“妈妈要买20千克大米,每千克2.3元钱,妈妈有50元钱够不够?”这样的问题只需要估算就可以,不必具体算出需要多少钱。而这样的问题,“一箱汽水24瓶,每瓶1.25元,买两箱需要多少钱?”就需要精确的计算,当然可以有不同的计算方法。
2、加强“数感”的培养
培养学生数感是新课程提出的重要目标之一。学生学习数学不只是学习数学事实,而且要了解数和运算的实际意义,用数及其关系表达和交流信息,用数学的观点解释现实问题。《标准》中对数感做了一个概括性的说明,”数感的具体体现是:能用数来表达和交流信息;理解数的意义,能运用自己熟悉的事物去体会较大的数或较小的数;能用多种方法来表示数;理解数之间的联系和相对大小关系;为解决问题而选择适当的运算,估计运算的结果,并能选择算法和工具进行运算”。 数感可以理解为人们主动地、自觉地地理解和运用数的意识。数感是数学素养的重要表现,它是建立明确的数概念和有效地进行计算等数学活动的基础,是将数学与现实问题建立联系的桥梁。
数感的培养应体现在数的认识、数的运算等内容的教学活动之中。《标准》在具体目标中提出,”结合现实素材,感受大数目,并能进行估计”。”体会数在日常生活中的作用,会运用数表示事物,并能进行交流”。这些目标都是建立数感的具体表现,需要在教学活动中着力培养。如,在认识大数目时,为学生提供丰富的现实背景,使学生在真实的情境中受到感染和体验。说一说你所遇到的大数的情境;估计一个操场大约有多少人;一个剧院大约能容纳多少人。看一段足球比赛的录像,感受一个体育场有几万人,一万人大约有多少?如果一个班40人,一所学校24个班,一所学校大约多少人?多少所学校大约是一万人?这样一些具体的、与学生生活实际密切联系的活动,可以使学生对数,特别是较大的数形成一个鲜明的表象,并且再遇到相似的情境时,在头脑中会有一个具体的参照物。
让学生从报刊上搜集一些真实的统计数据,或为学生提供一些数目较大的统计数据,会使学生了解大数的应用和学习大数的现实价值。
2001年中国人口统计:香港约有6200000人,台湾约有23000000人,澳门约有430000人,大陆约有1211210000人。
? 正常人一年内心脏可输出3220000克血液。
? 通讯卫星离地面35860千米。
? 蜻蜓的眼睛是由28000个小眼睛组成的。
? 一头奶牛一生约产奶1545400千克。
数感的形成不是通过一节课,一个单元,或一个学期的教学就能完成的,它是一个潜移默化的过程,需要用较长逐步培养。
3、提倡解题策略与计算方法的多样化
一个问题可以通过不同的策略找到答案,一个算式也可以用不同方式得出结果。用什么方式更合适,得到结果的合理性如何,与问题的实际背景有关系,与学生的思维方式和发展水平也有关。以往的数学教学中,过分强调解题方法的唯一性,或计算方法的最优化。而忽视了学生解决问题过程中不同的思考方式和不同的解决策略的探索。如下面几个例子。
例1:8+5=? 是不是一定要按照看大数(8),拆小数(5),然后用“凑十”的方法写成下面的形式再计算:
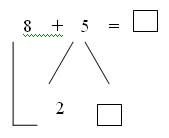
例2:“每箱汽水是24瓶,12箱这样的汽水一共多少瓶?”
学生可以列出算式 24 × 12 =?然后用不同的方法进行计算。也可以写成不同的算式来计算:
24×10+24×2
24×2+24×10
24×5+24×5+24×2
12×10+12×10+12×4
…… ……
也可以用竖式进行计算。不同的计算方法都可以得到问题的答案。学生可以通过讨论交流对
计算8+5=?时,学生可以用上面方法算,但也允许学生用其他的方法,如5+5=10,10+3=13; 8+1+1+1+1+1=13;8+4=12,12+1=13。
不同算法的看法。在此基础上,总结两位数乘法的计算方法和运算法则。运算法则是一种相对方便的方法,在具体运用的时候,也可以用不同的方法解决问题。
例3:“21个人要过河,每条船最多可乘5人,至少需要几条船?怎样乘船合理?”
这个问题就不是简单地计算21÷5就可以解决的。没有实际背景的情况下,学生只是简单计算21÷5=4……1,而在这个实际问题中,学生就要了解商4和余下的1是什么意思,4表示4条船,1表示如果4条船上都坐满5个人,还剩下1个人也需要一条船,因此必须用5条船才可以。而对这个实际问题来讲,这只是一种解决方法。还可以3条船上剩5个人,另外两条船上乘3个人。一条船上乘5个人,4条船上各乘4个人等。通过计算可以解决这个问题,但并不是只有一种方法找到答案,也不是只有一个唯一的答案。学生在探索实际问题的过程中,会切实了解计算的意义和如何运用计算的结果。
在具体的问题情境中,在实际的教学活动中,可能有不同的方法,不同的解题策略。有时学生的方法看起来可能比较“幼稚”,可能并不“聪明”,但这些方法是学生自己思考的结果,应当允许这样的方法。
解题策略和计算方法的多样化,不是简单的计算方法的问题,应当充分认识其教育价值,在教学实践探索合理的方式。
(1)解题策略和计算方法多样化为学生提供充分的思考问题空间
解决问题的过程是一个思考的过程。学生面对一个新的问题,首先想的是这个问题怎样解。一些已经熟悉的问题有固定的解题,而大量新问题并没有固定的解题模式。为学生提供问题情境,鼓励学生用不同的策略和方法解决问题,使学生有更多的自由思考问题的机会,有更多的探索余地。这有利于学生数学思考能力和解决问题能力的发展。
(2)解题策略和计算方法多样化有助于培养学生独立思考的能力
一个数学问题一般都有不同的解决方法和思考途径,即使计算的题目也有不同的方法。学生的思考方式和思维水平往往是不同的,教学过程中不应强求学生用统一的方法解题,特别是开始学习一类问题时,更应当让学生独立思考,探索解决问题的方法。
(3)学生之间有更多的交流与合作的机会
学生在探索解决问题方法的过程中,会发表不同的解题方法和策略。在自己说明解题方法和听取别人阐述解题方法的过程中,会增加学生之间的交流。特别是在解决那些比较复杂的、需要同学之间合作完成的问题时,更能促进学生之间的交流与合作。从不同的解题思路和方法中,学生可以获取更多的信息,提高解决问题的能力。
(4)提倡算法多样化并不是要求每一个学生都掌握多种方法
应当指出的是,提倡算法多样化,并不是要求每个学生都用不同的方法进行计算。学生可以用不同的方法解决问题,但更多的情况是不同的学生用不同的方法解决问题。强求统一的方法是不可取的,让每一个学生都用不同的方法计算,都能做到一题多解也不是应当提倡的。