当 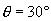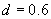， 时可得

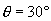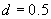当 ， 时可得

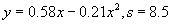
可见，同样的挑水角度，坡长越短，外喷半径越大。同理可分析坡长固定时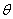， 越大，瀑布最高点增加，但外喷半径减小。这些从数学模型得到结果是符合实际的。

例 4 一类存储问题

问题分析

商店或工厂经常要存储一定量的商品或备件，因为如果存储量太少，可能会影响销售或生产，存储量太大，要为占用仓库和一些必要的保管措施而付出过多的费用 。因此，确定一个最优的存储量是必要的，这种问题便称为存储问题。常见情形有两种：不允许缺货的存储问题和允许缺货的存储问题；所谓不允许缺货是指问题要求所需物资随要随到，否则要造成重大损失。从存储性质上看还可分为确定性存储问题和随机性存储问题。这里仅介绍确定性且不允许缺货的存储问题。对于允许缺货情形见习题 。

模型假设
    1. 商品每天销售量为常数 。

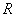2. 商品的进货时间间隔为常数 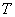，即每隔 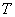天进货一次，且进货量为常数 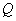，进货一次手续费也是常数 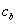；单位商品存储费 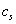元/天。