分别求解问题 ①、②。注意到问题 ② 无解 (因为 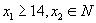 ,则第二个条件必不成立),故只需求解 ① 。仍采用以前解法有
,则第二个条件必不成立),故只需求解 ① 。仍采用以前解法有
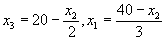 ,
,
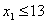 ,故得
,故得
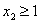
代入料头函数
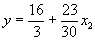
知当
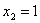 时,
时,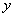 取最小值
取最小值
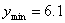 ,将
,将 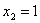 代入
代入
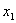 ,
,
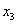 表达式可见
表达式可见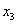 变成非整数解。再进行分支,再求解两次便得到
变成非整数解。再进行分支,再求解两次便得到
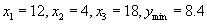
即为所求 。
这就是专用于求解整数规划问题的分支定界法 。应该指出的是,这里仅介绍了这个方法的基本思想,严格的做法请参看运筹学相关章节。
模型的进一步分析
1. 经过这样处理感到不太令人满意的是料头函数的最小值变大了。一般地,对同一个问题加限制性条件的结果必导至我们的目标值受损,这是很正常的。就本例来看,作为原来的条件(两个方程式)要求必须满足,那么要求整数解便只有使目标值受到损失,除非放宽条件。