充分利用问题的几何图形往往有助于模型的建立,这是不言自明的 。但确有相当一部分实际问题只需图示说明就足以解释实际现象,我们称这种建模方法为图示法。其特点是简明直观,因而受到人们的重视。图示法建模的实例在前述内容中已经出现,七桥问题便是一例。本讲再举一例以说明。
实物交换是人类发展史上一种重要的交换方式,在当今的社会生活中也是屡见不鲜的,这种实物交换问题可以出现在个人之间或国家之间的各种类型的贸易市场上 。 例如:甲乙二人共进午餐,甲带了很多面包,乙有香肠若干,二人希望相互交换一部分,达到双方满意的结果 。 显然,交换的结果取决于双方对两种物品的偏爱程度和需要程度,而对于偏爱程度很难给出确切的定量关系 。 我们将采用图示的方法建立实物交换的数学模型,确定实物交换的最佳交换方案 。
设交换的物品为 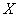 和 和 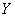 ,交换前甲占有 ,交换前甲占有 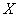 的数量为 的数量为 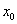 ,乙占有物品 ,乙占有物品 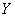 的数量为 的数量为 |
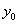 ,交换后甲占有物品 ,交换后甲占有物品 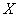 和 和 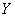 的数量分别为 的数量分别为 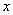 和 和 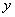 。 于是,乙占有 。 于是,乙占有 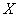 , ,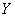 的数量为 的数量为 |
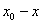 和 和 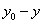 。 以 。 以 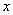 , ,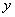 分别作为横、纵坐标建立平面直角坐标系,在 分别作为横、纵坐标建立平面直角坐标系,在 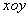 平面直角坐 平面直角坐 |
标系内,长方形 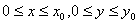 内任意一点的坐标 内任意一点的坐标 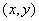 均代表一种可能的交换方案 。 均代表一种可能的交换方案 。 |
为了定量地描述甲、乙二人对物品 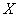 , , 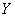 的偏爱程度,首先我们引入无差别曲线 。 的偏爱程度,首先我们引入无差别曲线 。 |
如果甲占有 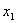 量的 量的 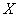 和 和 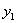 数量的 数量的 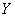 (图 2 — 3 中的 (图 2 — 3 中的 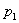 点)与占有 点)与占有 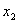 数量的 数量的 |
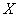 和 和 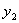 数量的 数量的 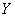 (图 2 — 3 中的 (图 2 — 3 中的 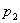 点)满意程度相同,则称 点)满意程度相同,则称 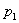 和 和 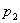 对甲是无差 对甲是无差 |
别的,或者说 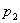 与 与 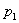 相比,甲愿意以 相比,甲愿意以 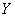 的减少 的减少 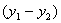 来换取 来换取 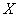 的增加 的增加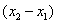 , , |
所有与 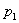 , , 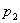 具有同样满意程度的点组成一条甲的 无差别曲线 具有同样满意程度的点组成一条甲的 无差别曲线 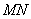 ,而比这些点满意程 ,而比这些点满意程 |
度更高的点,如 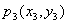 ,则位于另一条无差别曲线 ,则位于另一条无差别曲线 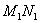 上 。 这样,甲就有无数条(一族)无差别曲线,不妨设为 上 。 这样,甲就有无数条(一族)无差别曲线,不妨设为 |