[ 答案 ] 根据平均声子数公式
|
[ 答案 ] 按照爱因斯坦的定义，爱因斯坦模型的格波的频率大约为 1013Hz，属于光学支范围，但光学支格波在低温时对热容的贡献非常小，低温下对热容贡献大的主要是长声学波，也就是说爱因斯坦没有考虑声学波对热容的贡献是这种偏差的根源。 |
| [ 答案 ] 合理。从声子能量方面来说，光学波声子的能量很大，它对应振幅很大的格波的振动，这种振动只有温度高时才能得到激发，故在甚低温下，晶体中不存在光学波。 |
[ 答案 ] 在甚低温下，不仅光学波得不到激发，而且声子能量较大的短声学波也不能被激发，只有声子能量较小的长声学波得到激发，即弹性波。而德拜模型恰只考虑了弹性波、对热容的贡献，因此，在甚低温下，德拜模型能与实验事实相符。 |
[ 答案 ] 根据平均声子数公式
|
| [ 答案 ] 对同一振动模式，温度高时的声子数目多于温度低时声子数目。 |
[答案]
|
[答案]
|
[ 提示 ] 根据频率分布函数公式
|
[ 提示 ] 德拜模型把晶体当作弹性介质来处理，弹性介质的振动模就是弹性力学中熟悉的弹性波，对于一定的波数矢量 q ，有一个纵波和两个独立的横波，它们的色散关系形式相同为
|
[答案]对于一维情况 ，
对于二维情况 ，
对于三维情况 ，
|
[ 答案 ] （ 1 ）原子间弹性恢复力常数为
一维简单晶格的色散关系为：
|
（ 2 ）
 ，其中
 。 |
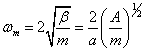（ 3 ）根据
 。 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
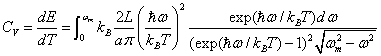章节练习>>> |
第二章┊ |
第三章┊ |
第五章┊ |
综合模拟┊ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
来判断。结论是在温度一定的情况下，一个光学波的声子数少于一个声学波的声子数目。 
，
，其中
。
。 
。对于
情况，有
。这里
时，
q 为虚值，表明这样的波在晶体中被阻尼，即晶体中不允许存在这样的振动模式，故 f
( ω )=0。 
和
，根据模式密度定义式 
可求解。对于纵波有
，对于横波有
，则总的模式密度为
，其中： 
。德拜模型认为存在德拜截止频
，且
。可以得到
，从而可以证明
。 
， 其中
， 可得
，其中
， 可得
，其中
，代入 β 表达式，即可得到
； 
，从而晶格热容为： 
，（ 2 ）一维晶格格波的频率分布函数 
。 
求证：频率分布函数为： 
，这里， 
为格波的
，试用德拜模型求一维、二维和三维情况晶体总的零点振动能。设原子总数为 N ，一维晶
。 
，试由简谐近似