[ 答案 ]二者是统一空间，倒格子空间的基矢是  ， 而波矢空间的基矢是  ；  分别为沿正格子基矢  方向晶体的原胞数目。倒格子空间中一个倒格点对应的体积为  ， 则波矢空间中一个波矢点对应的体积为  。 即波矢空间中一个波矢点对应的体积是倒格子空间中一个倒格点对应的体积的 1/N ， 由于 N 是晶体的原胞数目，数目很大，所以波矢点分布是级其稠密的，故在波矢空间作求和处理时，可把波矢空间内的状态点看成是准连续的。 |
| [ 答案 ]二者是统一空间，倒格子空间的基矢是 ， 而波矢空间的基矢是 ； 分别为沿正格子基矢 方向晶体的原胞数目。倒格子空间中一个倒格点对应的体积为 ， 则波矢空间中一个波矢点对应的体积为 。 即波矢空间中一个波矢点对应的体积是倒格子空间中一个倒格点对应的体积的 1/N ， 由于 N 是晶体的原胞数目，数目很大，所以波矢点分布是级其稠密的，故在波矢空间作求和处理时，可把波矢空间内的状态点看成是准连续的。 |
[答案] 布洛赫电子亦称“晶体电子”。晶体是由许多原子按周期性排列所构成，故晶体中电子受到周期性原子势场作用，其波函数被晶格周期势场调制，变成由周期函数所调制的平面波，称为布洛赫波。 |
[ 答案 ] 费米面是在绝对零度时，在波矢空间中被电子占据状态和不被电子占据状态的分界面。费米能级即是费米面所对应的费米能量，也是遵从“泡利不相容原理的费米子体系的化学势”。它近似代表费米子体系在某一温度下所占的最高能态。 |
[ 答案 ] 电子是基本粒子之一，带负电，电量为 1.602×10-19C,质量为9.1×10-31kg,自旋量子数为1/2；“空穴”是为了便于研究近满带电子行为而引人的概念，是一种假想的粒子，这种粒子带正电荷，具有正的有效质量mk*， 运动速度与 k 态电子相同。空穴的实质是近满带顶附近空的能量状态，即 k 态不为电子占据，则存在一个空穴。 |
[ 答案 ]
 ，
 ，
 |
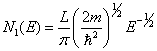[ 答案 ]
|
答案:
|
[ 答案 ] （ 1 ）势能平均值为
|
[ 答案 ]
|
[ 答案 ]
|
|
[ 答案 ] 12个格矢为： （
能带函数为：
|
|
[ 答案 ] 8 个格矢为 ：（
能带函数为 ：
|
[ 答案 ]  ； |
答案: ； |
[答案]带顶有效质量
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
章节练习>>> |
第二章┊ |
第三章┊ |
第五章┊ |
综合模拟┊ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
，所以有
，只取第一布里渊区（
）内的值，则
。 
；（ 2 ）势能曲线图如下： 
，
），（
），（
）； 
。 
）； 
； 带底有效质量
及 
可以计算三维情况能态密度，对于二维和一维情况，公式作相应的变
满足布洛赫定理。若晶格常数为 a
，电子的波函数为： 
来求平均值。 
的零级波函数。 
，则其属于第 n 个能带的条件是 
， 
，由此可以确定 n 和 m 的值，并按 
形式写出零级波函数。 
。 对于 s态波函数，是球对称，各方向的重叠积分相同，设为J1 
求带宽 ， 利用极值条件 
求极值 ； 利用 
求电子平均速度 ； 
求有效质量 。