1. 热动平衡条件
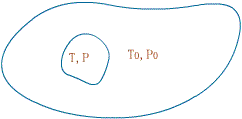
设有一个孤立的均匀系统.考虑系统中任意一个小部分.这部分虽小,但仍含有大量的微观粒子,可
以看作一个宏观系统.我们把这小部分称作子系统,而把系统的其它部分看作子系统的媒质.以不带
下标的量表示子系统的热力学量,带有下标 0 的量表示媒质的热力学量.例如 T 、 p 和 T 0 、
p 0 分别表示子系统和媒质的温度与压强.设想子系统发生一个虚变动,其内能和体积的变化分别
为 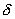 U 和 U 和 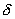 V 由于整个系统是孤立的,媒质的内能和体积应有相应的变化 V 由于整个系统是孤立的,媒质的内能和体积应有相应的变化 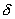 U 0 和 U 0 和 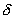 V 0, 使 V 0, 使
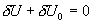
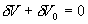
熵是广延量,虚变动引起整个系统的熵变 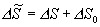
将 S 和 S 0 作泰勒展开,准确到二级,有
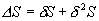
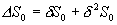
在稳定的平衡状态下,整个孤立系统的熵应取极大值.熵函数的极值要求
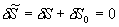
根据热力学基本方程
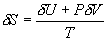 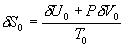
而 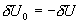 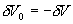
所以有 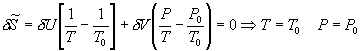
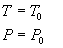
即达到平衡时系统中的任何部分与系统其余部分的温度和压强应该相等。
2. 稳定平衡条件
稳定平衡时要求 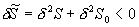
由于  , , 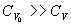 (相同的热量 (相同的热量 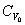 温度变化得很少) 温度变化得很少)
所以 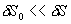 可忽略 可忽略 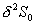
即要求 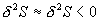
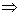 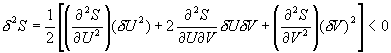
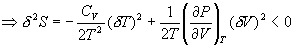
(证明:
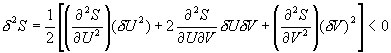
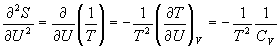
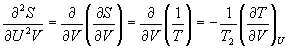
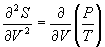
所以
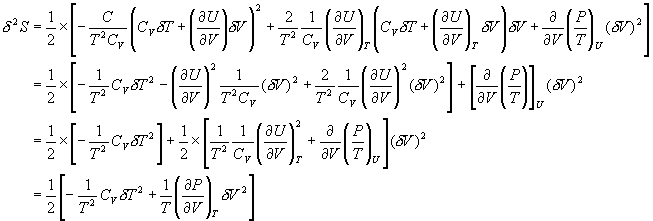
其中
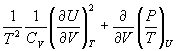 = = 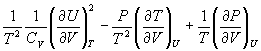
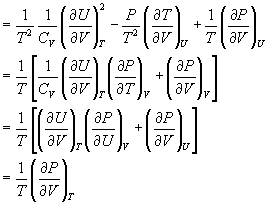
(证毕)
所以,要求 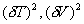 的系数小于零,则要求 的系数小于零,则要求
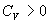 , , 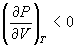 为平衡的稳定性条件。 为平衡的稳定性条件。
如果平衡稳定性条件得到满足,当系统对平衡发生某种偏离时,系统中将会自发产生相应的过程,以
恢复系统的平衡。

|
![]()