1. 范德瓦尔斯方程为:
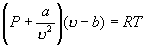
令 T 为不同的常量,作 P -- 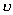 图,也有一临界点 图,也有一临界点
 ,如图 3.5 (1) 所示。 ,如图 3.5 (1) 所示。

图 3.5 ( 1 )
. 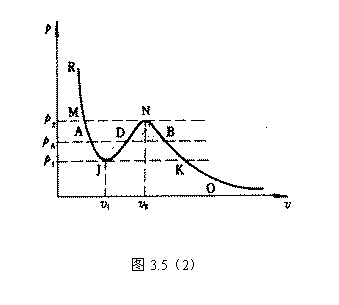
2、当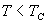 时,等温线也分为三个区域: OKB , BNDJA 和 AMR 。 A , B 与实验中的两相 时,等温线也分为三个区域: OKB , BNDJA 和 AMR 。 A , B 与实验中的两相
共存曲线的端点相对应, 如图 3.5(2) 所示。 在 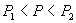 时,一个 P 对应三个 时,一个 P 对应三个 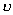 值。 曲 值。 曲
线 OKBAN , AMR 与实验一致。在 NJ 段, 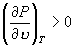 ,所以不可能实现。 BN 和 JA 段为亚稳态。 ,所以不可能实现。 BN 和 JA 段为亚稳态。
3. 分析各点的稳定性
摩尔吉布斯函数的全微分为
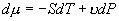
在等温线上有
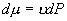
P 和 P 0 点之间的摩尔吉布斯函数,即化学势之
差为 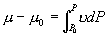 如果 如果
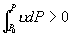 则 则 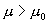 , ,
P 0 态比 P 态稳定。 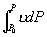 为等温线与 P 轴之间 为等温线与 P 轴之间 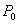 到 P 的面积。 到 P 的面积。
由图 3.5 ( 2 )可以看出,
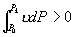 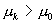 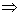 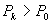
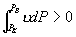 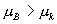 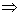 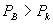
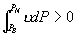 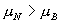 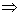 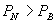
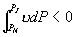  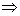 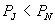
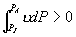 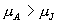 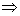 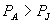
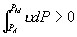 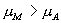 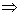 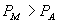
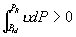 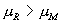 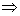 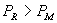
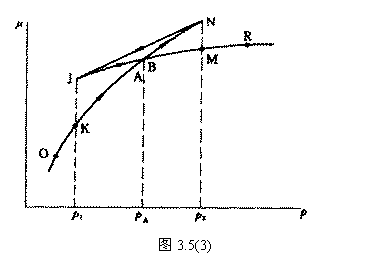
由于 A , B 为两同一相平衡曲线的端点,所以 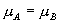 。各点化学势具体的数值由图3.5(3 ) 。各点化学势具体的数值由图3.5(3 )
给出。我们可以看出 OKBAMR 为稳定态, JN 为 不可能实现态, JA , BM 为亚稳定态。 4. 麦克斯韦积分法则
前边提到, A, B 对应于实验上两相平衡曲线的端点。麦克斯韦积分法则,给出了如何在范氏等温
线上确定 A, B 两点的方法如下: 由 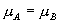 可知 可知
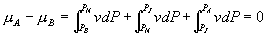
即为图 3.5(4) 中面积
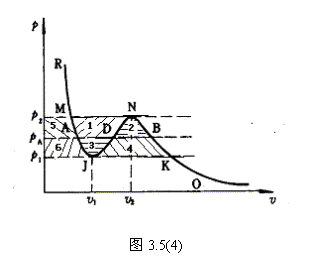
S 1 +S 2 +S 5 - S 1 - S 5 - S 3 - S 6 +S 6 =0 。 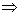 S 2 = S 3 S 2 = S 3
所以 AB 点的位置可由
面积( BND ) = 面积( DJA )确定。这种方法叫
做麦克斯韦积分法则。
5. 亚稳定平衡态
在 BN,AJ 上,  ,满足平衡稳定性要 ,满足平衡稳定性要
求, 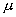 也较小,其中 A , B 点的一段在实验上可 也较小,其中 A , B 点的一段在实验上可
以观察到。所以为亚稳态。
AJ 为过热液体, BN 为过饱和蒸气。
6. 在 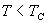 范围内,当 T 增加时, A 与 B 点接近; N 与 J 点接近。 范围内,当 T 增加时, A 与 B 点接近; N 与 J 点接近。
N 为极大值点, 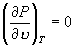 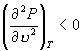
J 为极小值点, 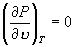 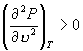
7. 当 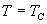 时, A 与 B 重合, N 与 J 重合,形成拐点。 时, A 与 B 重合, N 与 J 重合,形成拐点。
因此,临界温度 T C 和临界压强 P C 满足方程
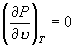 , , 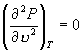
8. 临界系数
将临界温度 T C 和临界压强 P C 满足方程
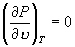 , , 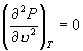
代入范氏方程,可得
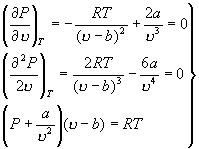
由此可解出
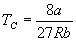 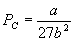 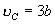
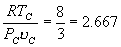
这一无量纲的比值叫临界系数。对各种气(液)体都相同。这个结果与实验值接近。
9. 对应态定律
引入 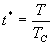 , , 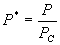 , , 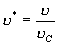
为对比温度,对比压强和对比体积,范氏方程变为
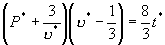
上式称为范氏对比方程。在这个方程中不含与具体物质性质有关的常数。这个结果叫对应态定律。

|
![]()