1. 单轴各向异性铁磁体
自旋取向只能沿着一个方向(正或负)序参量的能数为 1 。
2. 单轴各向异性铁磁体的能量
两个相邻原子在其磁矩平行时有较低的能量。
a. 基态,绝对零度  能量最低,原子号为固有磁矩,所有原子磁矩取向相同,完全有序。 能量最低,原子号为固有磁矩,所有原子磁矩取向相同,完全有序。
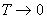 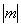 最大, m= ± m o 最大, m= ± m o
b. 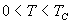
热运动有减弱有序取向的趋势 
c. 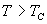 时 时
自发磁化强度为零,物质转变为顺磁状态。
3. 对称性破缺
在 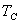 以上没有自发磁化,上下两个方向是对称的或等价的。 当温度变到居里点以下,这两个方向就不 以上没有自发磁化,上下两个方向是对称的或等价的。 当温度变到居里点以下,这两个方向就不
对称了,这是一种对称性 “ 破缺 ” 。
4. 序参量
自发磁化强度 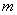 是一个标量,正号对应磁矩朝上,负号对应磁矩朝下。 是一个标量,正号对应磁矩朝上,负号对应磁矩朝下。
5. 与普通流体二级相变对应
m 对应于 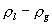  是标量,维数是 1 。顺磁相 是标量,维数是 1 。顺磁相 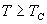 ,对应于液气不分。磁化强度朝上、 ,对应于液气不分。磁化强度朝上、
朝下分别对应于气态和液态。 |
![]()