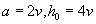
一齐代入 (1.24)式后，便可达到消去第四个变量 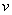的目的，从而得到 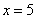。即 5 头牛才能在 6 个星期中吃完 6 亩地上的草。

模型分析与推广

本题中所作的假设的合理性值得研究，事实上，每头牛的吃草量，草的生长速度等均非常量。但在初中范围内这些假设应该被认为是合理的，否则本题至少需要微分方程等方法才能解释。

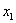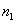可以将本问题提法更一般化从而更具一般性：设 头牛在 个星期中吃完 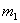亩地上的草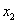， 头牛在 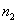个星期中吃完 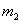亩地上的草，则要多少头牛才能在 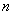个星期中吃完 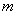亩地上的草。其模型应为

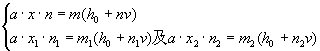
请读者试求解之。

例 2 套裁问题

为节省原材料，套裁是实际中常见一类问题 。如衣料套裁，钢材套裁等。类似这样的问题常见作法是，先筹划一些可行的方案，然后比较其优劣，选择其中一种或几种方案加以组合后再用数学方法加以处理，从而获得最佳的解决方案。
    塑钢窗厂要做 20 个矩形塑钢框，每个框由 2.2 米和 1.5 米的材料各两根组成。已知原料长 4.6 米，该如何下料，使用料最省？