这样,以一种平等、公正的方式选择 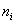 便是非常重要的事情了。如何确定尽可能公平(在数学上 便是非常重要的事情了。如何确定尽可能公平(在数学上 |
| 即不公平程度达到极小)的分配方案 ? |
设某校有 3 个系( 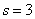 )共有 200 名学生,其中甲系 100 名( )共有 200 名学生,其中甲系 100 名( 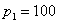 ),乙系 60 名 ),乙系 60 名 |
(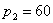 ),丙系40名( ),丙系40名(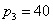 )。该校召开学生代表大会共有 20 个代表名额( )。该校召开学生代表大会共有 20 个代表名额(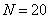 ), ), |
公平而又简单的名额分配方案是按学生人数的比例分配,显然甲乙丙三个系分别应占有 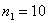 , , |
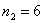 , ,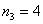 个名额 。这是一个绝对公平的分配方案 。现在丙系有 6 名同学转入其他两系学 个名额 。这是一个绝对公平的分配方案 。现在丙系有 6 名同学转入其他两系学 |
习,这时 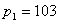 , ,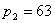 , ,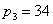 ,按学生人数的比例分配,此时 ,按学生人数的比例分配,此时 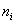 不再是整数, 不再是整数, |
而名额数必须是整数,一个自然的想法是:对 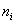 进行“四舍五入取整”或者“去掉尾数取整”,这 进行“四舍五入取整”或者“去掉尾数取整”,这 |
| 样将导致名额多余或者名额不够分配 。 因此,我们必须寻求新的分配方案 。 |
| Hamilton (哈密顿)方法 |
| 哈密顿方法具体操作过程如下: |
1. 先让各个单位取得份额 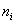 的整数部分 的整数部分 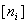 ; ; |
2. 计算 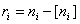 ,按照从大到小的数序排列,将余下的席位依次分给各个相应的单位, ,按照从大到小的数序排列,将余下的席位依次分给各个相应的单位, |
| 即小数部分最大的单位优先获得余下席位的第一个,次大的取得余下名额的第二个,依此类推,直至席位分配完毕 。 |
| 上述三个系的 20 个名额的分配结果见表 2 — 1 。 |