表 2 — 1 按哈密顿方法确定的 20 个代表名额的分配方案
系别 |
学生人数 |
所占比例（%） |
按比例分配的名额数 |
最终分配的名额数 |
甲 |
103 |
51.5 |
10.3 |
10 |
乙 |
63 |
31.5 |
6.3 |
6 |
丙 |
34 |
17.0 |
3.4 |
4 |
总和 |
200 |
100.0 |
20.0 |
20 |
哈密顿方法看来是非常合理的，但这种方法也存在缺陷 。 譬如当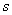 
和人数比例
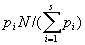不变时，代表名额的增加反而导致某单位名额 
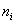的减少 。
考虑上述某校学生代表大会名额分配问题 。 因为有 20 个代表参加的学生代表大会在表决某些提案时可能出现 10 ： 10 的局面，会议决定下一届增加一个名额 。按照哈密顿方法分配结果见表 2 — 2 。
表2—2
系别 |
学生人数 |
所占比例（%） |
按比例分配的名额数 |
最终分配的名额数 |
甲 |
103 |
51.5 |
10.3 |
10 |
乙 |
63 |
31.5 |
6.3 |
6 |
丙 |
34 |
17.0 |
3.4 |
4 |
总和 |
200 |
100.0 |
20.0 |
20 |
显然这个结果对丙系是极其不公平的，因为总名额增加一个，而丙系的代表名额却由 4 个减少为 3 个 。
