| 由此可见,哈密顿方法存在很大缺陷,因而被放弃 。 20 世纪 20 年代初期,由哈佛大学数学家 Huntington (汉丁顿)提出了一个新方法,简述如下 。 |
| Huntington (汉丁顿)方法 |
易见, 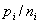 表示第 表示第 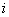 个单位每个代表名额所代表的人数 。很显然,当且仅当 个单位每个代表名额所代表的人数 。很显然,当且仅当 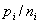 全相 全相 |
| 等时,名额的分配才是公平的。但是,一般来说,它们不会全相等,这就说明名额的分配是不公平的, |
并且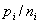 中数值较大的一方吃亏或者说对这一方不公平 。 同时我们看到,在名额分配问题中要达 中数值较大的一方吃亏或者说对这一方不公平 。 同时我们看到,在名额分配问题中要达 |
| 到绝对公平是非常困难的 。 既然很难作到绝对公平,那么就应该使不公平程度尽可能的小,因此我们 |
| 必须建立衡量不公平程度的数量指标 。 |
不失一般性,我们考虑 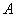 , , 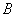 双方席位分配的情形(即 双方席位分配的情形(即 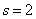 )。设 )。设 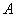 , ,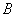 双方的人 双方的人 |
数为 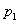 , , 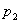 ,占有的席位分别为 ,占有的席位分别为 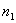 , , 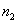 ,则 ,则 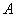 , , 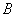 的每个席位所代表的人数分别为 的每个席位所代表的人数分别为 |
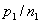 , , 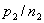 ,如果 ,如果 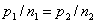 ,则席位分配是绝对公平的,否则就是不公平的,且 ,则席位分配是绝对公平的,否则就是不公平的,且 |
| 对数值较大的一方不公平 。为了刻划不公平程度,需要引入数量指标,一个很直接的想法就是用数值 |
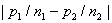 来表示双方的不公平程度,称之为绝对不公平度,它衡量的是不公平的绝对程 来表示双方的不公平程度,称之为绝对不公平度,它衡量的是不公平的绝对程 |
度。显然,其数值越小,不公平程度越小,当 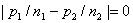 时,分配方案是绝对公平的 。 时,分配方案是绝对公平的 。 |
| 故用绝对不公平度可以区分两种不同分配方案的公平程度,例如: |
|
|