|
三、抽象、概括与具体化
表面现象是指事物的外部形态和外部联系,本质是事物的内部的矛盾运动、内部联系,本质隐藏在现象的背后,不能为人们直接感知。通过去粗取精,去伪存真,由此及彼,由表及里的过程,把本质的属性和非本质的属性区别开来,抽象出本质属性,舍弃非本质属性,这就是抽象。抽象是透过研究对象的表面深入里层,抽取出研究对象的本质属性的一种认识方法。
一般来说,抽象的过程分为分离、提纯、简略这几个基本环节。
1.分离,就是暂时不考虑研究对象与其他对象之间各式各样的总体联系。因为所研究的对象与其他对象有多种多样的联系,我们不可能对现象之间的各式各样的关系都加以考察,所以必须分离。
2.提纯,是指在思想中排除那些影响认识本质属性的干扰因素,使我们能在纯粹状态下对研究对象进行考察。
3.简略,就是对纯态考察的结果必须进行的处理。因为对考察结果的表述,只能简略地放映客观事实,它必然要撇开那些非本质的因素。
其实,一切科学都有一定的抽象性,但数学抽象性的特点体现得尤为明显。数学的抽象是对空间形式和量的关系这一特性的抽象,而这一特性是事物最一般的特性之一。所以,数学研究的抽象过程中,需要抛开较多的具体特性,因而具有较高的抽象性。数学中的概念、关系、定理等都是抽象的结果。例如,人类经过长期实践,逐渐认识到三只羊、三条鱼、三个孩子,三棵树的共同特性是“三”个东西,人们便从各种不同的具体事物中抽象出量的共同特征,即舍弃事物的具体内容而得到抽象的数:
数学的高度抽象性是因为数学有再抽象的特点,即需要逐级抽象而形成一个逐次提高的抽象过程。同样是数量之间的关系、或是空间关系,有些相对具体一些,有些则更一般、更抽象一些。例如,两点间距离,点到直线的距离,直线之间的距离等,这些距离概念具有一般性,但相对来说,还是比较具体一些。从这些距离概念中进一步抽出它们共同的一般特性,得出更一般距离的概念,这就是数学的再抽象。无论是在数学发展或是中学数学教学过程中,都要经常反复地进行再抽象。
在再抽象的过程中,允许有一定的跳跃性,比如从一般的单项式直接得出一般的多项式的概念,而且其间不一定需要更多的具体例子,可以直接拓广、上升到更一般的对象或关系。
数学的高度抽象性的又一个特点是大量使用抽象符号。抽象符号的使用,既增强了数学的精确化,也提高了数学的抽象性。
因为数学的高度抽象性使得学生在学习的时候经常遇到困难,比如初中生刚刚接触到负数,就很难理解。所以中学教学过程中必须充分注意数学抽象性的特点,以使学生能逐步适应数学的抽象性。
概括就是把抽象出来的若干事物的共同本质属性联合起来进行考察的一种思维方法。概括以抽象为基础,它是抽象的发展,抽象程度越高,概括性就越强,将概括所获得的概念、定理等运用于实际时,迁移的范围就越广。也就是说,高度的概括对事物的理解更具有一般性,获得的理论就更有普遍的指导性。
概括和抽象是思维过程中不可分割的两个方面。数学中的每一个概念都是对一类事物的多个对象通过观察和分析,抽象出每个对象的各种属性,再概括出各个对象的共同属性而形成的。数学的解题的规律和方法,也是通过分析、比较、抽象等思维的环节,最后进行概括的结果。所以数学的抽象程度最高,其概括性也最强。一般来说,我们谈到数学的抽象性时,往往包含了它的概括性。
例如,当引入了零指数、负整数指数幂的意义后,可把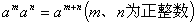 ; ; ,这两个性质可以概括为 ,这两个性质可以概括为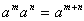 (m、n为整数)。 (m、n为整数)。
具体化是与抽象相对的概念。抽象是以具体作为基础,具体化则是把抽象概括出的性质应用于具体的过程。
数学内容的抽象性,往往掩盖了它们与具体内容间的关系。比如,学生刚刚接触函数的概念时,不仅名词生疏,形式抽象,而且还与具体内容格格不入,这是因为呈现给学生的只是知识的最终形态,而掩盖了它丰富的背景材料。甚至一些抽象的数学思想、数学方法也往往以十分现实、具体的事实为背景。对应,它是一个抽象的数学概念,也是一种重要的数学思想。其实,它早就孕育于原始人分配、狩猎或者数数的具体活动中。
这深刻说明:抽象与具体是相辅相成,互相转化的。现实的具体素材,是认识空间形式和量的关系的基础,是过度到抽象的概念和命题必不可少的初始环节,是理论思维的初级阶段。也就是说抽象性以具体性为基础,具体性不仅不妨碍过渡到抽象结论,而且还是抽象的理论思维的基础和保证。抽象性与具体性是密切结合的,不过,只有在数学内容的形成过程中它们才能很好地结合。由于数学理论的正确性标准是实践,研究数学的最终目的也是为了解决理论性或实践性问题。从抽象的数学内容进一步过渡到实践,即过度到更广泛、更丰富的具体对象,是认识空间形式和量的关系的更关键、更本质的阶段。这就说明,数学的抽象性不仅以具体性为基础,而且还以更广泛的具体性为其归宿。
总之,数学具有高度的抽象性,而抽象性又以具体性为基础,并以更广泛的具体性为其归宿。只不过数学中的具体性往往是相对的,而抽象性却有日益升级的倾向,但是,高度抽象的数学内容又可以凭借十分生动具体的材料做原型。也就是说,高度抽象的数学内容也有通俗化、形象化的可能。数学的抽象性和具体性是一对矛盾的统一体,处理好这一基本关系的主要途径,就是不能独立地讲授抽象结论,而应当讲清它们的来龙去脉,讲清它们的产生、形成和运用发展的过程。
中小学学生由于年龄较小,受到抽象思维的局限性,往往觉得数学很抽象,很难理解。这就需要数学教师借助具体的素材,从具体实例出发,分析讲解相对抽象的内容。另一方面,只要我们举出足够数量的具体例子,学生则立即乐于接受一些抽象的结论。事实上,只要和分数运算相对比,学生易于理解并掌握分式运算。只要以多位数乘法做实例并进行对比,学生易于掌握多项式乘除法的分离系数法。
可见,中小学数学教学要把握好抽象、概括与具体化思想的应用,结合学生思维的特点进行教学,这样有助于学生理解抽象结论,有助于提高教学质量和加快教学进度。
|