| 本章学习目标 | 本章学习要点 | 本章学习资源 | 本章思考题 | 本章参考书目 | |||||
|
第一节 数学命题 一、命题的意义 人们在社会实践中,产生概念之后,就要运用概念做出各种判断。例如,通过对有理数的研究,我们容易做出这样的判断: |
|||||||||
| 第四章详细目录 | 上页 下页 | ||||||||
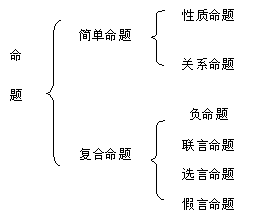
| 第一节 数学命题 一、命题的意义 二、命题的结构 三、命题演算 四、性质命题、关系命题 五、数学命题的四种形式及其关系 第三节 推理与证明 一、数学中的推理 二、数学中的证明 |
第二节 逻辑思维的基本规律 一、同一律 二、矛盾律 三、排中律 四、充足理由律 第四节 数学思维 一、数学思维的意义 二、数学思维的品质 三、数学思维的分类 |
||||||||
| 第一章 | 第二章 | 第三章 | 第四章 | 第五章 | 第六章 | 第七章 | 第八章 | 第九章 | 第十章 |