|
四、性质命题、关系命题
(一)性质命题
性质命题就是断定某事物具有(或不具有)某种性质的命题。例如:有些四边形是平行四边形;任何一个圆都不是直线形。
在性质命题中,虽然断定的事物具体内容不同,但都由主项、谓项、联项、量项所组成。命题的主项指的是指命题中表示判断对象的概念,逻辑学中通常用“S”表示。例如,矩形是平行四边形,“矩形”就是主项。
命题的谓项指的是指命题中表示判断对象的性质的概念,通常用“P”表示。例如上述命题中,“平行四边形”就是谓项。
命题中都有一个联系主项和谓项的关系词,我们称之为命题的联项,通常又被称为命题的“质”。例如“是”、“不是”、“能”、“不能”、“有”、“没有”。
在主项或是谓项前一般都由一个表示判断对象数量的概念,称之为命题的量项。如“一切”、“有的”。量项又称为命题的“量”,通常分为两种:全称量项(表示在一个命题中对主项的全部外延作了断定,通常用“所有”、“任何”、“一切”等词语表示,在命题的语言表达中可以省略)和特称量项(表示对主项的部分外延作了断定,常用“有的”、“某些”等词语表示,在命题的语言表达中不能省略)。例如:“矩形是平行四边形”中,“矩形”是主项,“平行四边形”是谓项,“是”是联项,对主项进行限定的量项“所有”被省略。
性质命题的基本逻辑结构是“所有(有的)S是(不是)P”。按照性质命题的“联项”,即“质”的不同,可以将其分为肯定命题(断定事物具有某种性质)和否定命题(断定事物不具有某种性质);按照性质命题的量的不同,可分为全称命题(断定某类中的每一个对象或某一个别对象是否具有某种性质)和特称命题(断定某类中的部分对象是否具有某种性质)。
按照性质命题中质和量的不同结合,可将性质命题分为如下四种:
1.全称肯定命题:断定一类事物的全部都具有某种性质的命题。通常用“A”表示。逻辑形式是:“所有的S都是P”。
2.全称否定命题:断定一类事物的全部都不具有某种性质的命题。通常用“E”表示。逻辑形式是:“所有的S都不是P”。
3.特称肯定命题:断定一类事物中的部分对象具有某种性质的命题。通常用“I”表示。逻辑形式是:“有的S都是P”。
4.特称否定命题:断定一类事物中的部分对象不具有某种性质的命题。通常用“O”表示。逻辑形式是:“有的S不是P”。
(二)关系命题
关系命题就是断定事物与事物之间关系的命题。例如,△ABC全等于△EFG;直线AB平行于直线CD。
关系命题由主项、谓项和量项三部分组成。主项又称为关系项,是指存在某种关系的对象。谓项又称关系,是指各个对象之间的某种关系。量项表示主项的数量。例如,直线AB平行于直线CD,“直线AB”是关系前项,“直线CD”是关系后项,“平行于”是谓项。
关系可以存在于两个或是两种事物之间,也可以存在于两个或是两种以上的事物之间。存在于两个事物之间的关系,通常称为二元关系。数学中常见的二元关系有自反关系、对称关系、传递关系。
1.自反关系:如果R是定义在集合S中的一个二元关系,且对每个x∈S,有xRx,则称二元关系R在S中是自反的。例如实数集合中的相等关系就是自反的。
如果在集合S中没有一个元素和自己具有关系R,则称二元关系R在S中是反自反的。
2.对称关系:设R是定义在集合S中的一个二元关系,对每个x、y∈S,如果xRy,就有yRx,则称二元关系R在S中是对称的。例如,直线集合中的平行关系、垂直关系等都是对称关系。
设R是定义在集合S中的一个二元关系,对每个x、y∈S,如果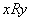 ,就必有 ,就必有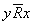 (即x和y不具有关系R),则称二元关系R在S中是反对称的。 (即x和y不具有关系R),则称二元关系R在S中是反对称的。
3.传递关系:设R是定义在集合S中的一个二元关系,对每个x、y、z∈S,如果xRy且yRz,就有xRz,则称二元关系R在S中是传递的。例如,实数集合中的相等关系、大于关系、小于关系等都是传递关系。
设R是定义在集合S中的一个二元关系,对每个x、y、z∈S,如果xRy且yRz,就有 (即x和y不具有关系R),则称二元关系R在S中是反传递的。 (即x和y不具有关系R),则称二元关系R在S中是反传递的。
|