|
第三节 推理与证明
在数学教学过程中,使学生了解并遵循正确的思维规律,掌握好推理和证明方法,也是使学生学好数学基础知识,提高基本能力的有效途径。
一、数学中的推理
根据命题间的关系,以一个或几个已有的命题得到一个新的命题的思维过程叫做推理。在推理过过程中,所根据的已有命题叫做推理的前提,得到的新命题叫做推理的结论。正确的推理要求前提真实,运用符号形式逻辑规律的推理形式,以期得到真实的结论。
推理是确定数学命题的真假不可少的方法。数学中常用的推理形式有演绎推理、归纳推理和类比推理三种。
(一)演绎推理
从一个或几个已有判断做出一个新的判断的思维形式叫做推理,其中已有的判断叫做推理的前提,做出的新判断叫做推理的结论。正确的推理要求前提必须是真实的,要求运用符合形式逻辑规律的推理形式,以求得到真实的结论。推理是确定命题真假必不可少的方法,数学中常用的推理形式有演绎推理、归纳推理以及类比推理。
1.演绎推理
演绎推理是从一般到特殊的推理,显然,演绎推理的前提判断范围包含结论中的判断范围。它是数学论证的一种主要形式。因为演绎推理含有两个前提和一个结论,所以又称三段论法,它的理论基础是下面的公理:如果集合M的所有元素具有(或不具有)性质P,如果x是集合M的元素(即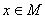 ),则x也具有(或不具有)性质P。三段论包括大前提、小前提、结论三个判断。它的一般形式是: ),则x也具有(或不具有)性质P。三段论包括大前提、小前提、结论三个判断。它的一般形式是:
大前提:集合M的所有元素具有(或不具有)属性P的一般判断;
小前提:集合 ,即S是M的子集; ,即S是M的子集;
结论:集合S的所有元素具有(或不具有)性质P。
在数学中常用三段论来进行推理,例如,用三段论来证明“等腰直角三角形的两个底角是45°”。
因为任意一个三角形的三内角之和是180°;
而等腰直角三角形是三角形,所以等腰直角三角形的内角和是180°;
又等腰直角三角形有一个角是直角,即90°;
所以等腰直角三角形的两底角之和是90°;
又因为等腰三角形的两个底角相等;
所以等腰直角三角形的两个底角是都是45°。
在这个论证过程中,三角形的内角和是180°是大前提,小前提是等腰直角三角形也是三角形,结论就是等腰直角三角形的内角和是180°。
演绎推理的前提必须是正确的,否则会推出错误的结论。如果前提正确,推理形式也正确,那么结论一定是正确的,这是演绎推理的优点。
(二)归纳推理
归纳推理与演绎推理的过程相反,归纳推理是从个别或特殊的事物所作的判断扩大为同类一般事物的判断的一种推理,有时也称归纳推理为归纳法。
根据归纳推理的前提和结论所做判断的范围是否相同,我们可以把归纳法分为完全归纳法和不完全归纳法。
1.完全归纳法
如果归纳推理的前提中一个或几个判断范围的总和与结论中判断的范围完全相同,则这种归纳推理叫做完全归纳法。
例如,在中学数学中,证明圆周角定理和余弦定理,用的就是完全归纳法;再比如证明三角形三条高线交于一点的定理时,就是先分别证出锐角三角形的三条高线交于一点、直角三角形的三条高线交于一点以及钝角三角形的三条高线交于一点,从而推出任意三角形的三条高线交于一点的结论,这个定理的证明思想也用到了完全归纳法。
完全归纳法是对一切可能情况都进行论证以后得出结论的,因此,这个结论必定是正确的。所以完全归纳法可以作为数学的严格推理方法。
用完全归纳法进行推理的时候,要注意前提的判断范围不要重复,也不要遗漏,亦即前提判断范围的总和不能小于结论判断的范围。
2.不完全归纳法
如果归纳推理的前提判断范围的总和小于结论判断的范围,则这种归纳推理叫做不完全归纳法。
在中学数学里经常会用到不完全归纳法,因为通过一些实例计算的结果、归纳概括出公式、定理、法则等,这样最容易为人所接受。比如在探求多边形内角和公式时,先对三角形、四边形、五边形的内角和进行考察,总结出算式的共同特点,从而归纳出n边形的内角和公式。
应当注意,不完全归纳法是不严格的,由它得出的结论,不一定是可靠的,一般只能作猜想和假定,要使它真实,还须加以实践检验或逻辑证明。
例如,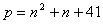 ,以 ,以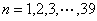 去检验p都是质数。如果由此得出结论:“n为任何自然数时,p均为质数”那就错了。因为当n=40时, 去检验p都是质数。如果由此得出结论:“n为任何自然数时,p均为质数”那就错了。因为当n=40时,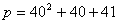 是合数。 是合数。
(三)类比推理
类比推理是以两个对象都有某些相同或类似的属性,并且其中一个对象还有另外的某些性质作为前提,从而推出另一个对象也有这些相同或类似属性的思维形式。类比推理是一种从特殊到特殊的推理,学生接受起来会容易一些,因此中小学数学常常把学习的新旧对象进行类比。例如把多项式的整除性与自然数的整除性进行类比,分式的性质和运算可以从分数的类比中推理。
但因为类比推理是一种特殊到特殊的推理,所以类比推理所得结论的真实性是不确定的,因此它不能作为数学的严格推理方法。不过,它可以给人们建立一种猜想,猜想的真实性有待进一步严格证明和实践检验。它与不完全归纳法得所出的结论,既有共性,又有差异性。共性就是说所推得的结论都是一种猜想,是否正确都有等于近一步检验;差异性就是说一个由特殊到特殊,一个由特殊到一般。
|