第八章 中小学数学教学的特殊规律

第一节 数学概念及其教学

    一、什么是数学概念

    概念是指反映事物的本质属性和特征的思维形式。比如，圆是一类事物，它是平面内到定点的距离等于定长的点的集合，这是圆的本质属性，而圆的概念就是这一本质属性的反映。
    客观世界的许许多多事物都有各种各样的性质，事物间存在各式各样的关系，这些性质和关系都是事物的属性。事物由于属性相同或不同，形成各种不同的类，属性相同的事物形成一类，属性不同的事物就形成不同的类。
    正确概念是科学抽象的结果。人们在实践活动中接受客观事物的各种各样的信息，形成观念，从而获得感性认识，在此基础上运用比较、分析、综合、抽象和概括等方法，去粗取精，舍掉事物的一些次要方面，保留了事物的本质属性，抽象出一类物事所具有而其它类事物所不具有的那些属性，即本质属性和特征，从而形成了反映事物的本质属性和特征的各种各样的概念。
    现实世界的空间形式和数量关系是数学的特定研究对象，数学概念就是反映这些数学对象的本质属性和特征的思维形式。例如，人们对太阳、满月等现实的圆形物体的形象得到了圆的感性认识，初步形成了关于圆的观念，在实践活动中，通过制造圆形工具或器皿需要画圆，从而逐步认识了圆的本质属性，最后形成圆的概念。在数学中，每一个概念通常都用一个特有的名称或符号来表示，例如，O表示以点O为圆心的圆，又如两个三角形全等用≌来表示。
    数学概念的产生与发展途径是多方面的。有的数学概念是从它的现实模型直接反映得来的。例如，几何中的三角形、梯形等概念都是从物体的形状、位置、大小关系等具体形象抽象概括得来的。又如，自然数概念是从绳子的条数，或其它单位事物集合元素的个数，或者从事物排列的次序抽象概括得来的。另外，有的数学概念是经过人们的加工，把客观事物的属性理想化、纯粹化才得到的。例如，直线这个概念所反映的“直”和“可以无限延伸”等特征是从笔直的条形物体的形象理想化、纯粹化得来的。还有些数学概念是从数学内部的需要中产生出来的。例如，无理数，它是在运用勾股定理计算以1和1为两条直角边的直角三角形斜边长时而得到的，由此引发了无理数的诞生。还有一些数学概念是根据理论上有存在的可能而提出来的。例如，自然数集、无限远点、无理数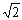等概念都是在一定的理论基础上提出来的。还有一些数学概念是在一定的数学对象的结构中产生出来的。例如，多边形的顶点、边、对角线、内角、外角等概念都是从多边形的结构中得出来的。
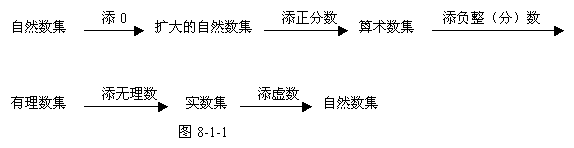
    数学概念是不断发展、变化的。这是因为，一方面事物的本身是发展变化的，因此，反映事物的概念也要随之而发展、变化；另一方面，由于人们的认识是不断深化的，因而关于事物的概念也要发生变化。如数的概念的形成就是一个逐步发展的过程（如图8-1-1所示）。
    对角的概念的叙述也是不断深化的。在平面几何中，角的概念是这样定义的：具有公共端点的两条射线所组成的图形叫做角。但对于现实生活中会出现的720°或-1440°等不在0°到360°的角，这样定义的角就不太适合了，因此，平面三角中，对角的概念又进行了扩充：一条射线绕它的端点旋转所成的图形叫做角，并规定按逆时针方向旋转形成的角叫做正角，按顺时针方向旋转形成的角叫做负角，这样角就有了正负之分，并将角扩充到了全体实数。

    概念是非常基本、非常重要的。因为有了概念才可以运用概念进行判断和推理，才可以进行论证，不可设想一个没有关于圆的概念的人，能做出关于圆的命题、推理和证明，因此，要掌握一门科学，首先要掌握这门科学的概念。此外，判断是由概念构成的，推理是由判断构成的，论证又是由判断和推理构成的，因此，概念这种思维形式是其他思维形式的基础，从这个意义上来说，概念是思念的细胞。