|
二、定理的教学
数学中定理的教学过程一般分为定理的引入、定理的证明、定理的记忆以及定理的应用四个阶段。定理的教学要求首先应使学生明确它的条件和结论,然后寻找证明思路和掌握证明的方法,以及如何应用它们进行推理和解决实际问题。
1.定理的引入
一般而言,命题的引入可以分为两种形式。一种是直接向学生展示命题,教学的重点放在分析和证明命题以及命题的应用方面。另一种是通过演算、实验或实物展示等手段,让学生自己思考,猜测命题的内容,之后再给出严格的证明。
比如,向学生提出一些供研究、探讨的素材,并作必要的启示引导,让学生在一定的情境中独立进行思考,通过运算、观察、分析、类比、归纳等步骤,自己探索规律,建立猜想和形成命题。后一种方法因为有了学生主动参与,积极思维,在“活动”中获取知识,因此更有利于学生对定理的记忆。
比如在讲三角形内角和定理时,可以让学生做一个三角形的模型,然后剪下其中的两个角,并将它们与第三个角拼接,在直观上这三个角构成了一个平角,即和是180°,实际上这种实验还暗示着内角和定理的证明方法。
2.定理的证明
定理引入后,教师的重点工作转向对定理的条件、结论剖析,探讨其证明思路,这也是定理教学的一个难点和重点。因为教材上的定理大多只给出证明的过程,但并没有对这种证明方法发现的过程加以叙述,此时教师的任务不是简单地将教材中的证明过程照搬到黑板上,这样的照本宣科是不能解决学生的疑虑的。因此,教师应该仔细地分析证明过程,并揭露推理过程中每一个环节如此进行的缘由,并启发学生寻找问题解决的方法。
3.定理的记忆
定理是后续学习的基础,也是以后证明、推理、计算以及解决实际问题的需要,因此,需要学生牢固掌握定理的内容。但这并不是要求学生们对定理只进行形式上的死记硬背,否则,记忆的结果只能让定理成为毫无意义的文字堆积。
要避免这一点,就首先要做到让学生明白定理得出的缘由,也就是定理简单的证明过程;其次,在证明新定理或者在解题之前,恰当地进行有系统的关于定理及它们间联系的复习,可以帮助定理的记忆和理解它们之间的关系。
4.定理的应用
一般而言,数学中的定理是包含程度较高的命题,应用它们可以解决众多的数学问题。同时,定理的应用又是训练学生的逻辑推理能力、发展学生思维能力的必由之路,因而,定理的应用是命题教学中必不可少的重要环节。
一个定理向学生呈现之后,要给学生指出一些满足定理的正确的例子,可以既有基本训练题,又有巩固知识的题型,还可以包括综合型的题目。另外还应适当地补充一些逆用、变用定理及公式的例题、习题,以培养学生活用、逆用命题的能力。新的教学理念要求知识的综合性,所以应该编拟一些应用定理来解决物理、化学等其它学科问题的题的题型。同时也要指出由于不具备某些条而不适合定理的反面例子,使学生懂得定理的条件对定理的结论的制约性。
数学定理应用的教学包括以下几个方面:
① 定理和公式成立的条件与使用的范围。学生在学习定理和公式时,往往忽视它们成立的条件和使用的范围,产生各种错误。因此在进行定理和公式应用的教学时,应特别强调定理和公式在一定条件下与一定的范围内才能使用。
例如,已知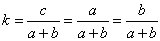 ,求k ,求k
对于这道题,许多学生会直接应用等比定理,得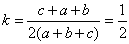 ,这样解的同学就忽视了定理成立的条件—分母之和不为零,所以该题的正确答案应由两个,即,当 ,这样解的同学就忽视了定理成立的条件—分母之和不为零,所以该题的正确答案应由两个,即,当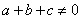 时, 时,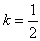 ;当 ;当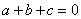 时,k=-1。忽视定理、公式的成立条件而产生错误,是同学们学习中的一种普遍现象,这一点应引起我们广大教师的高度重视。 时,k=-1。忽视定理、公式的成立条件而产生错误,是同学们学习中的一种普遍现象,这一点应引起我们广大教师的高度重视。
② 定理和公式的各种基本应用。对于定理和公式所解决问题的几种基本类型,要通过例题分别加以说明。
③ 定理和公式的灵活应用。在掌握定理和公式的正向运用的基础上,掌握它们的逆向运用,进一步还要掌握它们的各种变形的应用。可以以不同层次的题组、变式训练等形式,由浅人深的在不同的层次上应用定理。
④ 定理和公式的引伸和拓广。根据学生的水平,适当对所学的定理和公式进行引伸和拓广,以拓宽学生的视野,加深对定理和公式的理解,提高创造性思维能力。
|