三、公式的教学

    因为公式就是定理，所以定理的教学法完全适合于公式的教学，但公式又是特殊的定理，因此也存在着一些它自身具备的教学法：

    （一）高度重视公式的推导
    因为公式的推导不但能帮助公式的记忆，而且有助于提升它们推理能力的水平，以及知识的迁移能力，也就是用公式的推导法来解决类似的数学问题。

    （二）公式的形式特点
    这也是帮助公式记忆与正确运用的必要方法。比如公式：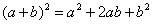　　
    应当指出，这个公式共含3项；都是正号；系数按1，2，1排列；a的数由2次按降幂排列，而b的指数按升幂排列。

    （三）公式的变形
    因为公式通常是一个等式，因此可以做一些恒等变形，根据未知量和已知量的要求进行变换，因此要对公式进行灵活运用。比如。公式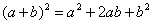由左到右是对整式做乘法，而由右到左，是对式子进行因式分解。

    （四）公式的条件是公式存在的前提
    学生运用公式发生错误的原因之一就是忽略条件．例如算术根的运算法则必以各个算术根存在为前提；又如对数运算法则以各对数有意义为前提等．在教学中教师要抓住学生作业中的典型错误，加以分析，以期引起注意．

    （五）要在体系中掌握公式
    这要分三种情况来考虑：　　
    第一种情况：有的公式在以后还要发展。如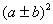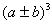，以后要发展为二项式定理；又如勾股定理以后要发展为更为广泛的余弦定理。
    第二种情况：要注意公式的正、反使用。如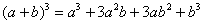，从左到右使用是作为乘法公式使用，而从右到左使用是作为因式分解使用。只有左、右两方面都会使用才算熟练掌握公式。
    第三种情况：不能平均使用力量，而要抓住主要的。
    例如对于解一元二次方程，有开平方法、因式分解法(包括十字相乘法)、配方法、公式法。这四种方法如果一个个平铺直叙地讲，虽然也把主要方法交待了，但显得不够。另一种讲法，就是突出十字相乘法及公式法，这从实用的意义来说要比前一种讲法进步些，但真正的实质仍未交待清。
    事实上，从因式间的因果关系看，因式分解法是最主要的。因为所谓的开方法就可归之因式分解法。配方法可归之开平方法，从而也可归之因式分解法．公式法是从配方法的基础上推导得到的，因而它的根源仍是因式分解法。但从公式的应用角度看，应以因式分解法与公式法并重。公式法虽然对有解的二次方程来说是个一般的方法，但有时并不简单，如果辅之以因式分解法，那么在解二次方程时就会得心应手了。

    附：三角形内角和定理的证明教学案例

    一、课题：三角形内角和定理的证明
    二、教材：义务教育课程标准实验教科书数学（7-9年级，北京师范大学出版社）八年记下册第六章第6.5节 三角形内角和定理的证明
    三、教学目标
    1．感受证明的含义，了解证明的含义、了解证明的必要性。
    2．了解命题、定理的含义，会区分命题的条件(题设)和结论。
    3．体会在证明中添加辅助线的必要性以及便捷性；初步了解“数”与“形”，培养数形结合思想。
    四、教材分析
    1．内容分析
    本节内容新课程标准实验教科书各个版本都有安排，北京师大版将其安排在八年级下册第六章证明（一）中的第5节。
    在此之前，学生通过拼图曾经探索过这个结论，已经感受过这个结论的正确性；同时，学习了关于命题的有关知识；而且，他们还知道，通过观察、度量、猜测得到的结论不一定是正确的！在本节内容之后，学生将要学习三角形内角和定理的推论以及有关三角形、四边形有关基本性质的证明。在这节内容中，学生第一次接触添加辅助线的方法，而辅助线在证明中的重要性不言而喻！
    因此，这节内容在初中数学“空间与图形”中承上启下，对今后的学习有良好的奠基作用。
    2．教学重点：以三角形内角和定理的证明为载体，学习几何证明思想，以及辅助线的有关知识，体会数形结合思想。
    3．教学难点：辅助线添加的必要性和具体方法：
    （1）为什么要添加；（2）在哪里添加；（3）如何添加；（4）哪种添加方法最简。
    五、设计思路分析
    三角形内角和定理是学生接触较早的定理之一，其内容和应用早已为学生所熟悉。因此，本节课需要重点解决的问题是定理的证明；在定理的证明中，学生将首次接触和应用辅助线，于是，在证明中“为什么要添加辅助线”、“如何添加辅助线”就成为这节课的重中之重！
    因此，本节课的基本定位在于，通过三角形内角和定理证明的教学，具体实践和感受几何证明的思想，体会辅助线在几何问题解决中的桥梁作用！同时，引领学生体会数学中的重要思想——数形结合思想。
    首先，我从学生已有的生活经验入手，创设情境，让学生体会生活中桥梁的重要性，同时引出搭建桥梁的注意事项。然后，把生活中的桥向数学中的“桥”引申，借助“撕三角形纸片、拼接、验证三角形内角和定理”的过程分析，启发诱导学生初步体会辅助线及其在证明中的作用。最后，引领学生进一步体会辅助线添加方法的多样性，渗透“最优化”思想。
    六、教学环节设计
    1．创设情境
    从生活中的桥的作用引入，引发学生思考桥的作用，进而导出数学中也有这样的“桥”！向学生提出如下问题串，达到目的：
    ①刚才在校门口，有位老爷爷问我：“从兴宁区到江南区怎么走？”如果是你，你该如何告诉他？
    （方式很多，但是在现实生活中，不管你以何种方式去，都必然要跨越——邕江，而跨越邕江最便利的方式就是过——桥！）
    ②桥在我们生活中都起到怎样的作用呢？（联系河流的两岸）
    ③南宁市有几座桥？从哪座桥走最省事？（突出过桥有多种选择，同时有最省方案。）
    ④你认为架桥要注意什么问题呢？（地点有选择）
    设计说明：南宁市地形的突出特点是，一条河流（邕江），将城市一分为二。目前，南宁市区的桥梁共有5座（含在建中的），因此，对南宁市区学生来说，桥梁不仅熟悉，而且，也时常感受到桥梁给生活带来的便利。南宁市的兴宁区和江南区位于河流两岸，任课教师通过这两个区来设问，旨在突出桥梁的作用。一连串问题串的提出，都是为了即将接触和学习的辅助线埋下伏笔。
    当学生回答并思考这些问题后，他们对生活中的桥的问题已经有了一定得认识。此时，教师指出：在我们数学的学习中也存在这样的“桥”，你注意到了吗？
    设计说明：这就促使学生去思考：数学中的桥是什么样子啊？它是否也象生活中的桥一样有用？我怎么没有注意到呢？这将大大激发学生的求知欲，为后面的探究作好铺垫。
    2．分析命题
    （1）教师提出三角形内角和定理的证明问题。
    （2）组织学生回顾“撕三角形纸片、拼接、验证三角形内角和定理”的过程。
    （3）提出，“能不能通过其他的方式，达到平移其中的两个内角，进而证明三角形内角和定理”的问题。
    （4）分析三角形内角和定理的已知和未知，指出命题中的已知和未知相当于桥的两岸。辅助线是连接两岸的“桥”！
    ①数的研究
    对于三角形的内角和是180度这样一个结论，启发学生回想：我们在小学时是怎样知道这个结论的？
    （通过量角器进行角度的测量，这就是“数”的研究，量角器在这里起到桥的作用）。
    提出进一步的问题：通过前两节课的学习，我们知道：通过观察、度量、猜测得到的结论不一定是正确的！测量会产生误差！问题解决得并不完美！这就促使我们去寻求新的研究方向——形！(体会证明的必要性)
    ②形的研究
    启发学生回顾上节课学习的有关证明的内容，导出“平移三角形内角的办法”：
    （我们学习了有关命题的知识，学习过验证一个命题正确性的一些方法，但是，如何才能从数学上真正证明“三角形内角和定理”这个结论的正确性？请同学们回忆：要证明一个命题我们首先要做的工作是什么？——分析命题的条件和结论！条件相当于已知，结论相当于未知。（理解命题）结合表格从形来分析已知与未知，提出问题：“用什么将两者联系起来？在哪里进行联系？怎样联系？”
    结合“数”与“形”进行分析。

命题	三角形三个内角的和等于180°			方法
分析	已知	桥	未知
	三角形三个内角的和		等于180°
数	∠A、∠B、∠C的度数相加	量角器	等于180°	测量
	三个角拼在一起	辅助线	①平角；②两角互补	证明
		①如何添线（如何架桥） ②在哪添线（在哪架桥） ③有几种添法（可架几座桥） ④哪种最简捷（哪座桥最省）		如何证明

    3．分组探究
    （1）教师组织学生分组讨论：有了上面的知识作为铺垫，我们可以开展探究活动了，看那组最先找到解决办法，找到的方法最多。
    （2）在学生开展探究的过程中，教师参与其中，对个别感到困难的小组可以进行适当的提示和引导。着重从下列问题去引导：
    ①如何添线（如何架桥）——添线的目的是将三角形的三个角向一个平角或互补的两个角转化。
    ②在哪添线（在哪架桥）——可以选择三角形的顶点、边上或三角形的内部甚至外部。但在学生探究时注意分层次引导，由学生自己发现地点选择的多样性。
    ③有几种添法（可架几座桥）——从地点上看可以有若干种，同时出于对平角或互补的选择又有不同。
    ④哪种最简捷（怎样架最省）——体会数学中的最优化思想！培养学生学数学，用数学的意识。
    （3）教师指导学生添加辅助线，给出完整地“三角形内角和定理”的证明！
    4．成果展示
    教师指导学生进行大班回报：
    · 借助实物投影仪，将学生找到的添加辅助线的方法进行汇总展示。注意选取不同的方法。
    · 在展示过程中，注意关注学生的表达以及寻找到的添加辅助线的方法，若有不全的，教师进行必要提示。
    · 引导学生将辅助线添加在三角形的顶点上、边上及三角形内、外部均可以！然后，进一步引导学生比较，哪种最好？（最省）

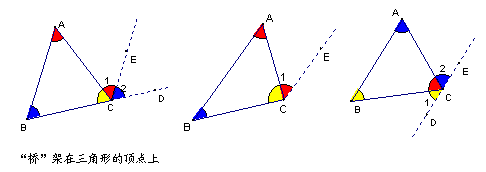
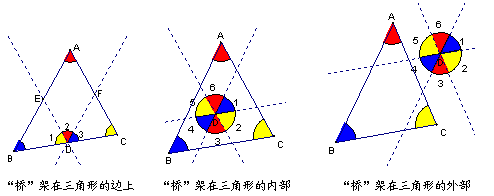
    设计意图：给学生充分的自我展示的机会！尽量发现更多的添加辅助线的方法。
    5．归纳、总结
    教师引导学生从如下四个方面进行小结：
    ①是否积极地参与了本节课的探究活动？你的工作是否获得本组组员的肯定？
    ②三角形内角和定理的证明掌握了吗？添加辅助线要注意哪些问题？
    ③“桥”的作用以及“架桥”思想，数与形谁好？ “数形结合”思想。
    ④此外，你在这节课上还有什么收获？体会？
    6．课程结束
    （1）布置作业
    证明：四边形的内角和等于360度。
    （2）最后，让我们用我国著名数学家华罗庚的诗句来结束我们的这节课：
    数形本是相倚依，
    焉能分作两边飞 ?
    数缺形时少直觉，
    形少数时难入微，
    数形结合百般好，
    隔离分家万事休，
    几何代数统一体，
    永远联系莫分离。
    七．点评：作为“几何证明”的重要组成部分，这节课所涉及的内容对于证明的学习显得十分重要。其原因，一方面在于，这是添加辅助线、进行几何证明的首次，学生对此普遍感到困难；另一方面，这是《全日制义务教育数学课程标准》下的“几何公理体系”的第一次循环的综合运用，即“两条直线平行，内错角相等”、“内错角相等，两条直线平行”公理的综合运用。
    作为设计者和教学的实际执行者来说，对这篇案例的设计师是精心的，尤其是从“数”与“形”两个角度对辅助线作法的分析、探讨，是成功的。当然，对于这节课的教学目的，设计者将教材上的规定的教学目标“掌握“三角形内角和定理”的证明及其简单应用；对比过去撕纸等探索过程，体会思维实验和符号化的理性作用；通过一题多解、一题多变等，初步体会思维的多向性，引导学生的个性化发展”修改为前文的教学目标，从设计者的意图来说，是合理的，但作为“创造性用教材”的角度，还是值得推敲的。