三、数学问题的类型

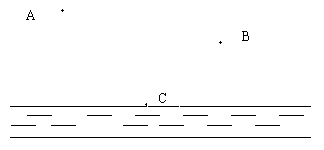
    问题是数学的心脏，知识、能力、思想、观念等都是在解决问题的过程中形成和发展起来的。数学问题种类很多，但用于数学问题解决教学的问题大致有以下三种，它们具有不同的教育价值和功能。

    （一）可以构建数学模型的实际问题

    数学不止是锻炼人心智的工具，人们越来越强调它在现实生活中的应用价值。生活、生产中的实际中的很多问题都可以抽取出来，通过构建数学模型，化实际问题为数学问题，然后应用数学方法或数学思想来给予解决。比如这样一道题：一位小牧童，从A地出发，赶着牛群到河边饮水，然后再到B地，问当怎样选择饮水地点时，才能使牛群所走的路程最短？

    （二）探究性问题

    要通过一定的探索、研究去深入了解和认识数学对象的性质，发现数学规律和真理的问题叫探索性问题。对这种问题的教学，需要采用类似于科学研究的方式让学生去探索、获取知识。数学中的数量关系、图形性质及其变化规律，数学公式、法则、命题、定理等虽然都是间接知识，教师不可能完整的呈现知识的产生与发展过程，但知识形成、发展过程的意义却可以让学生重新建构。培养他们的数学思维能力，科学的探索精神。

    （三）开放性问题

    开放性问题是相对于数学课本上有明确条件和结论的封闭型问题而言的，它在问题的条件、结论、解题策略或应用等方面具有一定开放程度的问题，这类问题不一定有解，答案也不一定唯一，所给的条件也可能是多余的，但开放性问题并不等于随意性的问题，结论仍然要求确定、精确。这类数学问题的解决就是要让学生在探索的过程中进一步理解所学的知识，培养他们思维的灵活性、发散性，从而达到培养他们的创新精神、创新意识的目的。
    特别指出的是，对于数学问题，我们要注意区分“问题”和“习题”，前者实际上指的是“problem”,后者大多指“question”。
    一般的中小学数学教材的习题有三种类型：一种是安排在各个小节的“练习”，是直接应用新知识和新技能进行解答的题目；第二种是各章的每一大段教材之后的“习题”，比“练习”题复杂些，更能体现基本概念、基本定理、基本方法的应用；第三种是每章末的“复习参考题”和“总复习参考题”，这类题目有一部分属于综合题，难度较大，涉及的知识面也较广，富于变化，带有一定的灵活性和技巧性。
    中小学数学教材中的习题一般是条件充分、结论确定、解法典型、供巩固知识的练习用。这些习题是为数学教学和日常训练等设计的，适合于学习知识、训练技能。而“问题”不仅包括教科书上的习题，也应包括那些来自实际的问题；不仅应包括“单纯练习题式的问题(routine problems)”，也应包括“非单纯练习题式的问题(non-routine problems)”；不仅应包括条件充分、结论确定的问题，也应包括条件不充分、结论不确定的开放性问题和具有探索性的问题。“问题”适合于学习发现和探究的技巧，适合于进行数学的原始发现以及学习如何学。因此，两者的外延、所要达到的学习目的大不相同。
    虽然习题与“问题”有一定的区别，但并不否认习题在数学教学中的作用。为了使学生理解数学概念、定理、法则，全面系统地掌握数学知识，提高解题的技能、技巧，习题有着不可取代的作用。