三、概念间的关系

    所谓概念间的关系就是概念的外延间的关系。在形式逻辑中，根据概念间的外延有无重合之处，概念间的关系可分为相容关系和不相容关系。

    （一）概念间的相容关系

    所谓概念间的相容关系是指两个至少有一部分外延重合的概念间的关系，它又分为部分重合和完全重合。因此，概念间的相容关系又可分为同一关系、属种关系和交叉关系三种。
    1．同一关系。也叫全同关系，指如果两个概念的外延完全重合，则这两个概念之间的关系是同一关系。概念的同一关系可用图8-1-2表示（A、B表示两个概念）：
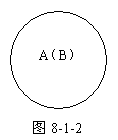
    例如，无理数和无限不循环小数的就是两个内涵不同，但外延完全相同的概念。但具有同一关系的两个概念，它们的外延虽然完全重合，但是它们的内涵可以不同。比如等腰三角形底边上的高线、中线以及顶角平分线的外延都是同一条线段，而它们的内涵却各不相同。
    研究概念间的同一关系，可以对概念所反映的对象得到较深刻、全面的认识。另外，在推理证明过程中具有全同关系的概念可以互相代换，可以使论证变得简明。
    2．属种关系。不是同一关系的两个概念，如果其中一个概念的外延完全包含另一个概念的外延，那么这两个概念就具有属种关系。在具有属种关系的两个概念中，外延较大的那个概念叫做属概念，外延较小的那个概念叫做种概念。概念的属种关系可用图8-1-3表示：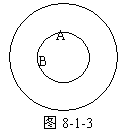
    具有属种关系的两个概念，由于各个概念在这种关系中所处的地位不同，在逻辑学中又把属概念叫做上位概念，把种概念叫做下位概念。例如，实数和有理数是具有属种关系的概念，而且由于实数的外延完全包含有理数的外延，因此实数是属概念（或上位概念），而有理数是种概念（或下位概念）。应当指出，属概论和种概念是相对的，如平行四边形是矩形的属概念，但它又是四边形的概念。另外，作为一个概念的属概念未必是唯一的，它的种概念也未必是唯一的，比如平行四边形、四边形和多边形都是矩形的属概念；而矩形、菱形、正方形又是平行四边形的种概念。
    具有属种关系的两个概念，它们的外延和内涵在数量上存在互相制约的关系。即属概念和种概念之间，一个概念的内涵越多，则它的外延越小；反之，一个概念的内涵越少，则它的外延越大，这种关系叫做内涵与外延的反比关系，变称“反变关系”。根据这种反变关系可知，种概念具有它的属概念的一切性质，而且还具有它自己特有的属性，这种关系在研究概念的性质以及推理、证明中经常用到。
    3．交叉关系。如果两个概念的外延有且只有一部分重合，那么这两个概念之间的关系就是交叉关系，又称部分重合关系。这种交叉关系可用图8-1-4表示，其中A、B两个概念的外延既有相同部分也有不同部分。

    交叉关系在数学中常常见到，也经常被用到。例如菱形和矩形就是交叉概念，交集为正方形概念的外延；又如等腰梯形和直角梯形是交叉概念，它们的交集为等腰相角梯形。又如在方程组或不等式组的解集，以及几何中的轨迹交截法都用到概念的交叉关系。

    （二）概念间的不相容关系（也叫全异关系）

    所谓概念间的不相容关系就是指属于一个属概念中的两个在外延上没有任何重合部分的种概念之间的关系。概念的不相容关系又分为矛盾关系和反对关系。
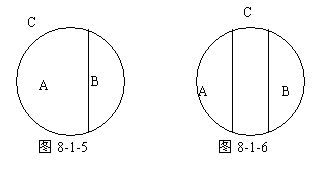
    1．矛盾关系。在同一属概念之下的两种概念，如果它们外延的和等于属概念的外延，而且这两种概念具有全异关系，那么这两种概念的关系称为矛盾关系。可以用图8-1-5表示这种关系，其中A、B两个部分表示具有矛盾关系的两个概念的外延，这两部分没有任何共同的部分，而且加起来等于属概念C的全部外延。例如整数和分数相对于有理数来说就是矛盾关系。
    2．反对关系。在同一属概念之下的两个概念，如果它们的外延的和小于属概念的外延，而且这两个概念具有全异关系，那么这两个概念的关系称为反对关系或者对立关系。反对关系可用图8-1-6来表示，其中A、B两个部分表示具有反对关系的概念的外延，这两部分完全没有相同的地方，但两者之间和小于属概念C的全部外延。例如正实数和负实数相对于实数而言，就是反对关系。