|
二、数学中的证明
(一)何为证明
数学证明是根据已被确定正确性的公理、定理、定义、公式、性质等数学命题来确定某一数学命题真实性的推理过程。
从逻辑结构来分析,任何证明都是由论题、论据、论证三部分组成。其中论题是指需要确定其真实性的那个命题,比如证明“平行四边形的两组对边分别相等”就是一个论题,任何论题都包含条件和结论两部分。论据是指被用来作为证明论题的理由、依据,包括给定的条件和证明论题真实性所引用的数据,以及公理、定理、定义、公式、性质等命题。论证即证明的过程,也就是进行一系列推理的过程。
(二)证明的规则
证明既要保证证明的准确与逻辑的合理性,又要使证明具有说服力,为此证明必须遵守如下的五条规则:
规则1:论题必须明确
论题是所要论证的对象,因此论题要清晰,不能让人产生歧义,如果论题本身含糊不清,就无法进行证明。比如“有两条边和一个角对应相等的两个三角形全等”这个论题就是含糊不清的。论题中所说的角究竟是两相等边的夹角还是邻角并不确定,因此也就无从证明,这种错误叫“论题不清”。
规则2:论题应当始终如一
这就是说,在整个证明的过程中,论题应该始终保持如一,不得随意改变,否则就会出现“换题论证”的错误。比如证明四边形的内角和等于360°,如果采用正方形来代替一般四边形加以论证,这就是犯了“换题论证”的错误。
规则3:论据必须真实
论据是用来证明论题真实性依据,但如果论据本身就是虚假的,那么由此得出和论题的真实性就不成立,违反这条规则的逻辑错误叫“虚假论据”,在几何论证中,这种错误常常表现在,滥用不成立的命题作为论据,或者引用的定理与论题无关。
规则4:论据不能依靠论题来证明
论题的真实性是从论据的真实性而推出的,是依赖于论据来证明的。但如果论据的真实性反过来又要从论题的真实性而得出,那么结果什么也没有得出,违反这条规则的逻辑错误被称为“循环论证”。
规则5:论据必须能推出论题
每一个论证都是推理,证明过程必须运用有效的推理形式,因而论据必须是推出论题的充足理由,否则就会犯“推不出”的逻辑错误。
(三)常用的证明方法
根据题中给的已知条件和所要求证的结论不同,证明的方法也是多种多样的,因分类标准不同,证明方法的类别也不同。
1.按论题的命题形式来区分,有直接证法和间接证法
(1)直接证法
由命题的题设出发,根据一些已知的公理、定理等命题,通过若干次的推理,一直推到所要求的结论,像这样的证明方法叫直接证法,这是数学中最常用的证明方法。
(2)间接证法
对于有些命题,如果采用直接法,会使得证明的过程过于繁难,思考的过程也比较复杂,甚至利用的已证定理的所需条件并不充分,这时就采用间接法。间接法又分为反证法和同一证法。
①反证法:一个命题和它的逆否命题是等价的,因此,在证明某一命题时用直接法不易着手时,可以转而去求证它的逆否命题是真实的,这就等于证明原命题是成立的,这种证明的方法就叫做反证法。
反证法通常所采用的形式是,从结论的反面入手,假设结论的反面是真实的,那么由此引出的结论将与所给定的已知条件,或公理、定理等矛盾,说明假设是不成立的,因而结论是真实的。用反证法能简化证明的一个原因就在于,假设结论的反面是真实的,那么此时相当于多了一个已知条件,因此会使证明容易进行。
②同一法:如果一个命题符合同一原理,那么它的逆命题与它的真值性相同,因此,当一个命题不易直接证明,但它却符合同一原理时,就可以转而求证它的逆命题成立,即可得出原命题正确。
例 已知:在△ABC中,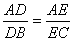 ,求证: ,求证: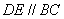 。 。
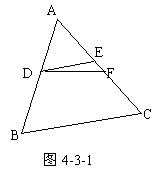 |
证明:过D作DF∥BC交AC于F。那么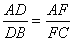 ,但已知 ,但已知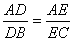
∴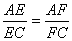
∴
即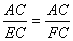 ∴
∴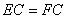
∵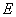 和 和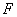 都在 都在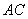 上, 上,
∴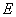 和 和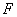 重合,从而 重合,从而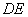 和 和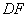 重合, 重合,
即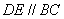 |
2.按论证的思维方式来分,有综合法和分析法
(1)综合法:在命题的推导过程中,综合法是从已知条件出发,逐步推理到要证明的结论,也就是由因导果。但是由于所导出的结论往往不唯一,所以就会出现很多的思路,而且选哪一条路子更合适,往往无从选择,只能逐一进行考虑,最终找到可行的证明途径。
(2)分析法:与综合法相反,用分析法在思考问题时,是从结论出发执果索因,追溯它能成立的条件,再就这些条件分别研究它成立又需要什么条件,直到所需条件都已知时,便找到了解题的通道了。
3.按论证的推理方法来区分,有完全归纳法、不完全归纳法、演绎法、数学归纳法
前三种方法在前面已经提到过了,所以这里对数学归纳法略作介绍原理,它适用于证明与自然数n有关的命题。这种方法的推导过程,一般是先用不完全归纳法从特殊的判断推广到一般的判断,然后根据归纳原理来证明这个一般判断。数学归纳法的证明通常采用以下的步骤:
①要证明命题对于自然数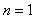 时是成立的; 时是成立的;
②假设当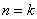 时,命题是正确的,然后以此为依据,推导出当 时,命题是正确的,然后以此为依据,推导出当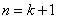 时,命题也成立; 时,命题也成立;
③得出结论,命题对于所有的自然数都是正确的。
需要注意的是,有些关于自然数的命题,并不是对所有的自然数都成立,而是对于大于或等于某一自然数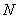 ( (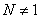 )的所有自然数都真实,在用数学归纳法证明这样的命题时,要在第一步验证当 )的所有自然数都真实,在用数学归纳法证明这样的命题时,要在第一步验证当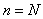 时,所证的命题是真实的。 时,所证的命题是真实的。
|
