五、数学命题的四种形式及其关系

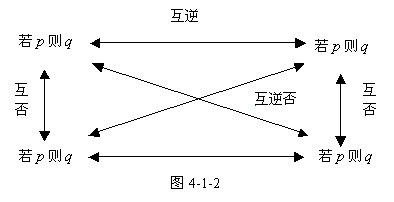
    （一）数学命题的四种形式

    在数学科学中，为了更加全面地研究命题中条件和结论的逻辑联系，往往把一个命题的条件和结论换位，或者把条件和结论变为它们的否定，这样就可以得到三个新命题。例如，以“若两角是对顶角，则此两角相等”为原命题，交换原命题的条件和结论的位置，就得到“若两角相等，则此两角是对顶角”，称为原命题的逆命题。否定命题的条件和结论，就得到“若两角不是对顶角，则此两角不相等”，称为原命题的否命题。否定原命题的条件和结论，并交换它们的位置，就得到“若两角不相等，则此两角不是对顶角”，成为原命题的逆否命题。
    如果用，分别表示对A、B的否定（即A、B不成立），那么有：
    原命题：；
    逆命题：；
    否命题：；
    逆否命题：。

    （二）四种命题的关系

    从上面四种命题的表达形式，我们可以知道：
    原命题和逆命题是互逆的，否命题和逆否命题也是互逆的；原命题和否命题是互否的，逆命题和逆否命题也是互否的；原命题和逆否命题是互为逆否的，逆命题和否命题也是互为逆否的。
    四种命题之间的关系，我们可以用下面的图示来表示：

    上述命题的真假，有着一定的逻辑关系。

    例1、原命题： 若两个三角形全等，则这两个三角形等积。（真）
    逆命题： 若两个三角形等积，则这两个三角形全等。（假）
    否命题： 若两个三角形不全等，则这两个三角形不等积。（假）
    逆否命题：若两个三角形不等积，则这两个三角形不全等。（真）

    例2、原命题：两条直线和第三条直线相交，若两直线平行，则同位角相等。（真）
    逆命题：两条直线和第三条直线相交，若同位角相等，则两直线平行。（真）
    否命题：两条直线和第三条直线相交，若两直线不平行，则同位角不相等。（真）
    逆否命题：两条直线和第三条直线相交，若同位角不相等，则两直线不平行。（真）

    例3、原命题：若一个四边形是平行四边形，则它的对角线互相垂直。（假）
    逆命题：若一个四边形的对角线互相垂直，则这个四边形是平行四边形。（假）
    否命题：若一个四边形不是平行四边形，则它的对角线不互相垂直。（假）
    逆否命题：若一个四边形的对角线不互相垂直，则这个四边形不是平行四边形。（假）

    从上述例子可以看出，互逆与互否的两个命题的真实性并非一致的，可以两个都真，也可以两个都假，也可以一真一假；而互为逆否的两个命题的真实性却总是一致的，同真同假。这种同真同假的关系，我们称之为等效关系。
    在中学数学教学中，要注意到学生往往学过一条定理后，自以为是的认为它的逆命题也真，因而给论证带来错误。